Gleichung einer Tangente,die eine Ellipse berührt

Question

Aufgabe: Ermittle Gleichungen jener Tangenten an die Ellipse ,die den Richtungsvektor g haben und gib die Berührungspunkte an!

Ell: x^2+4y^2=116    , g=(5/-1)

Problem/Ansatz:

Wie kann ich solche Frage lösen?

Answer 1

Du kannst die Gleichung auch sofort nach \(x\) ableiten:$$x^2+4y^2=116 \\ 2x + 8yy' = 0$$Aus der Vorgabe des Richtungsvektor folgt \(y' = -\frac 15\). Das setzt man in die Ableitung ein$$ 5x - 4y = 0 \implies y = \frac 54 x$$und erhält eine Beziehung zwischen \(x\) und \(y\).

Die gelbe Gerade im Bild ist der Graph von \(5x - 4y = 0\). Das kann man natürlich wieder in die Ellipsengleichung einsetzen$$\begin{aligned} x^2+4\left( \frac 54 x \right)^2=116 \\ \frac {29}4 x^2 = 116 \\ x_{1,2} = \pm4\end{aligned}$$und man erhält das Ergebnis für die Punkte \(P\) und \(Q\). Die Gleichungen für die beiden Tangenten \(t_{1,2}\) (rot) lauten dann$$t_{1,2}: \quad x = -\frac 15(x \mp 4) \pm 5 = -0,2 x \pm 5,8$$

Answer 2

Ell: x^2 + 4·y^2 - 116 = 0

g: y = b - 0.2·x

Wir setzen g in Ell ein

x^2 + 4·(b - 0.2·x)^2 - 116 = 0

1.16·x^2 - 1.6·b·x + 4·b^2 - 116 = 0

Die Diskriminante (D = b^2 - 4·a·c) der quadratischen Gleichung müsste 0 sein.

(1.6·b)^2 - 4·(1.16)·(4·b^2 - 116) = 0

538.24 - 16·b^2 = 0 --> b = ± 5.8

Also sind die Tangenten

t: y = - 0.2·x ± 5.8

Answer 3

Forme die Gleichung der Ellipse nach y um. Dann hast du zwei Funktionen f₁ und f₂.

Die Steigung der Tangente t_i ist -1/5 (i ∈ {1,2}). Die Tangente hat also die Funktiongleichung

        t_i(x) = -1/5·x + n_i

und du musst noch die n_i bestimmen. Das machst du indem du das Gleichungssystem

        f_i(x) = t_i(x)
        f_i'(x) = t_i'(x)

löst.

Comments

Forme die Gleichung der Ellipse nach y um.

Mach das besser nicht.

Answer 4

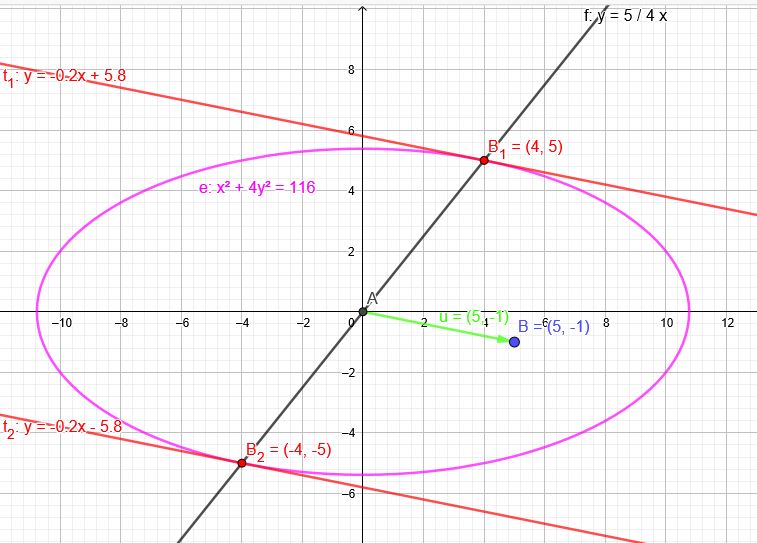
Ell: \(x^2+4y^2=116\)  Gerade durch A und B :\(y=- \frac{1}{5}x \)  mit \(m=- \red{\frac{1}{5}} \)

 \(e(x,y)=x^2+4y^2-116\)

\(e_x(x,y)=2x\)

\(e_y(x,y)=8y\)

\(e'(x)=- \frac{e_x(x,y)}{e_y(x,y)}=-\frac{2x}{8y}=-\frac{x}{4y}\)

\(- \red{\frac{1}{5}} =- \frac{x}{4y}\)      \( y=\frac{5}{4}x\)

Diese Gerade schneidet die Ellipse in den beiden Berührpunkten.

Nun noch beide Tangenten berechnen.

Comments

Nun noch beide Tangenten berechnen.

Du hast wirklich goldenen Humor.
Gut, die beiden Berührungspunkte zu kennen ist schon mal hilfreich, wenn man deinen umständlichen Weg wählt. Wie berechnest DU denn die Tangente, wenn sie dir nicht von Geogebra vorgegeben wird?

---

Tangente 1:

\( \frac{y-5}{x-4}=-0,2 \)

\( y-5=-0,2(x-4)=-0,2x +0,8\)

\( y=-0,2x +5,8\)

Tangente 2: analog

---

Woher weißt du denn den Anstieg -0,2 (ohne ihn bei Geogebra abgelesen zu haben)?

---

Der Richtungsvektor hat \(m= \frac{-1}{5}=-0,2 \)