Zunächst einmal gibt es genau dann ein eindeutige Lösung in einem LGS der Art$$A \cdot x = b$$wenn die Determinante der Matrix \(A\) nicht gleich 0 ist.
Bei der Matrix, die in der Aufgabe gegeben ist, ist es völlig egal, welches der neun Elemente man ändert, es verändert immer den Wert der Determinante. Man erhält also in jedem Fall ein Gleichungssystem mit genau einer Lösung. Einen der Werte der rechten Seite zu ändern bringt, wenn überhaupt, nur ein Gleichungssystem mit unendlich vielen Lösungen.
Im Allgemeinen ist das aber nicht der Fall. Um sich sicher zu sein, wählt man ein Element und berechnet die 'Untermatrix' dieses Elements (den korrekten Ausdruck dafür kenne ich nicht!). Die 'Untermatrix' soll die Matrix sein, die übrig bleibt, wenn man alle Elemente weg lässt, die in der gleichen Spalte oder Zeile des gewählten Elements stehen.
Also nehmen wir als Beispiel \(a_{23}\) - also die \(1\) rechts - dann ergibt sich:
$$\begin{pmatrix} \colorbox{#ffff00}{5}& \colorbox{#ffff00}{-2}& -4 \\ 1& 2& \colorbox{#ff88ff}{1} \\ \colorbox{#ffff00}{7}& \colorbox{#ffff00}{-10}& -11 \end{pmatrix} x = \begin{pmatrix} 7\\8\\-7 \end{pmatrix} \\ \implies \det(23) = \left| \begin{array}{rr} 5& -2 \\ 7& -10\end{array}\right| = 5\cdot(-10) - 7\cdot (-2) = -36 $$
Der Wert dieser 'Untermatrix' ist -36 - also \(\ne 0\). War die Determinante der Ausgangsmatrix vorher \(=0\), so wird nach der Änderung von \(a_{23}=1\) in irgendeinen anderen Wert, die Determinante nicht mehr 0 sein und das LGS eine eindeutige Lösung haben.
Was steckt dahinter? Man kann eine Determinante auch nach einer Zeile oder Spalte entwickeln, also nach dem Laplaceschen Entwicklungssatz berechnen. Für dieses Beispiel sähe das so aus, wenn man nach der dritten Spalte entwickelt:
$$ \begin{aligned} \det &= -4\left|\begin{array}{rr} 1& 2 \\ 7& -10\end{array} \right| - 1 \left|\begin{array}{rr} 5& -2 \\ 7& -10\end{array} \right| -11 \left|\begin{array}{rr} 5& -2 \\ 1& 2\end{array} \right| \\ &= -4 \cdot (-24) - \colorbox{#ff88ff}{1} \cdot(-36) - 11\cdot 12 \\ &= 0 \end{aligned} $$
Es liegt auf der Hand, dass bei einer Änderung der markierten 1, das Ergebnis sich verändert, da der Faktor neben der 1 \(\ne 0\) ist.
Eine alternative Betrachtungsweise:
Man kann sich die drei Spaltenvektoren der Matrix \(A\) als Vektoren im Raum vorstellen, so wie in folgender Szene dargestellt
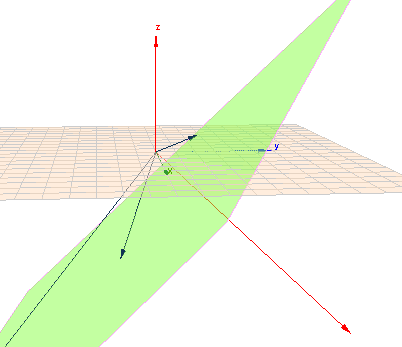
Alle drei (schwarzen) Spaltenvektoren liegen hier in einer Ebene (grün). Der Vektor \(b\) der rechten Seite ist rot dargestellt. Die Lösung so eines LGS besteht nun darin, eine Linearkombination der drei Spalten zu finden um nach \(b\) zu kommen. Wenn aber die drei in einer Ebene liegen und \(b\) nicht in derselben Ebene liegt, so ist das nicht möglich!
Eine Änderung genau eines Elements der Matrix \(A\) bedeutet die Änderung einer Koordinate eines der drei Vektoren. Es ist offensichtlich, dass diese Änderung so erfolgen muss, dass der gewählte Vektor die Ebene verlässt. Und das geschieht am besten dadurch, dass sich die Änderung in Richtung des Normalenvektors \(n\) der Ebene vollzieht. Der ist in diesem Fall$$n = \begin{pmatrix} 5\\ 1\\ 7\end{pmatrix} \times \begin{pmatrix} -2\\ 2\\ -10\end{pmatrix} = \begin{pmatrix} -24\\ 36\\ 12\end{pmatrix}$$\(n\) ist also im wesentlichen in Richtung der Y-Achse ausgerichtet, da der Y-Wert den größten Betrag hat; das Vorzeichen spielt keine Rolle.
Wenn man also von irgend einem der drei Spaltenvektoren den Y-Wert ändert (d.h in der 2.Zeile der Matrix), wird dieser Vektor sicher die Ebene verlassen und die Determinante wird nicht mehr 0 sein.
Spezialfall: Sollten zwei der drei Spaltenvektoren linear abhängig sein, so muss immer ein Wert bei einem dieser beiden Vektoren verändert werden.
Gruß Werner