Geometrie: Aussage über Viereck beweisen

Question

Aufgabe:

 In einem Viereck ABCD ist ein Kreis mit dem Mittelpunkt O einbeschrieben. Zeigen Sie, dass ∠AOB +∠COD = 180 Grad.

Vielen Dank:)

Answer 1

Jede Gerade durch einen Eckpunkt des Tangentenvierecks und \(O\) ist auch gleichzeitig Winkelhalbierende des Winkels in diesem Eckpunkts.

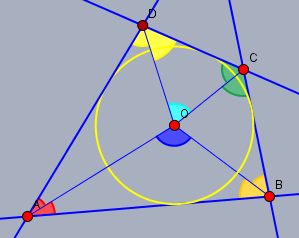
Die Summe aller Halbwinkel ist folglich 180°, da die Winkelsumme im Viereck 360° beträgt. Die Summe aller Winkel in den beiden Dreiecken \(\triangle ABO\) und \(\triangle CDO\) ist ebenso 360°. Beide Dreiecke zusammen enthalten genau einen Satz aller Halbwinkel des Vierecks. Folglich ist die Summe der verbleibenden Winkel \(\angle AOB\) (blau) und \(\angle COD\) (hellblau) die Differenz \(360° - 180°=180°\)

Answer 2

(1) α+β+γ+δ=360°. Wenn es eine feste Winkelgröße φ gibt mit β+δ=φ (schwarze Benennung), denn muss auch α+γ=φ (rote Benennung) sein. Dann gilt  (2) β+δ=α+γ. (2) in (1) eingesetzt, ergibt 2β+2δ=360° oder β+δ=180°. Bleibt allwrdings zu zeigen, das es dieses φ überhaupt gibt.