Trigonometrische Funktion Identität Beweisen

Question

ich soll die Identität von der Folgenden Gleichung zeigen:

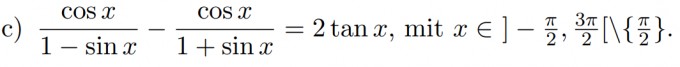
Mein Ansatz:

Ich habe versucht von der linken Seite aus die rechte Seite zu zeigen.

Zuerst habe ich die Brüche auf den gleichen Nenner gebracht und vereinfacht.

Ich erhalte dann:

$\frac{2*cos(x)sin(x)}{1-sin^2(x)}$

Nun weiß ich leider nicht, wie ich das vereinfachen koennte.

Über jegliche Tipps und Hilfe bin ich sehr dankbar.

MfG

Answer 1

Mit dem trig. Pythagoras: $1-\sin^2(x) = \cos^2(x)$

Somit ergibt sich $\dfrac{2\cos(x)\sin(x)}{\cos^2(x)} = \dfrac{2\sin(x)}{\cos(x)}= 2\,\dfrac{\sin(x)}{\cos(x)}=2\tan(x)$

Comments

Danke für die Hilfe. Hatte den trig. Pythagoras gar nicht im Kopf.

Answer 2

Es gilt doch : 1-sin²x=cos²x

Comments

Oh man. Das hab ich ja vollkommen vergessen das es existiert. Vielen Dank.