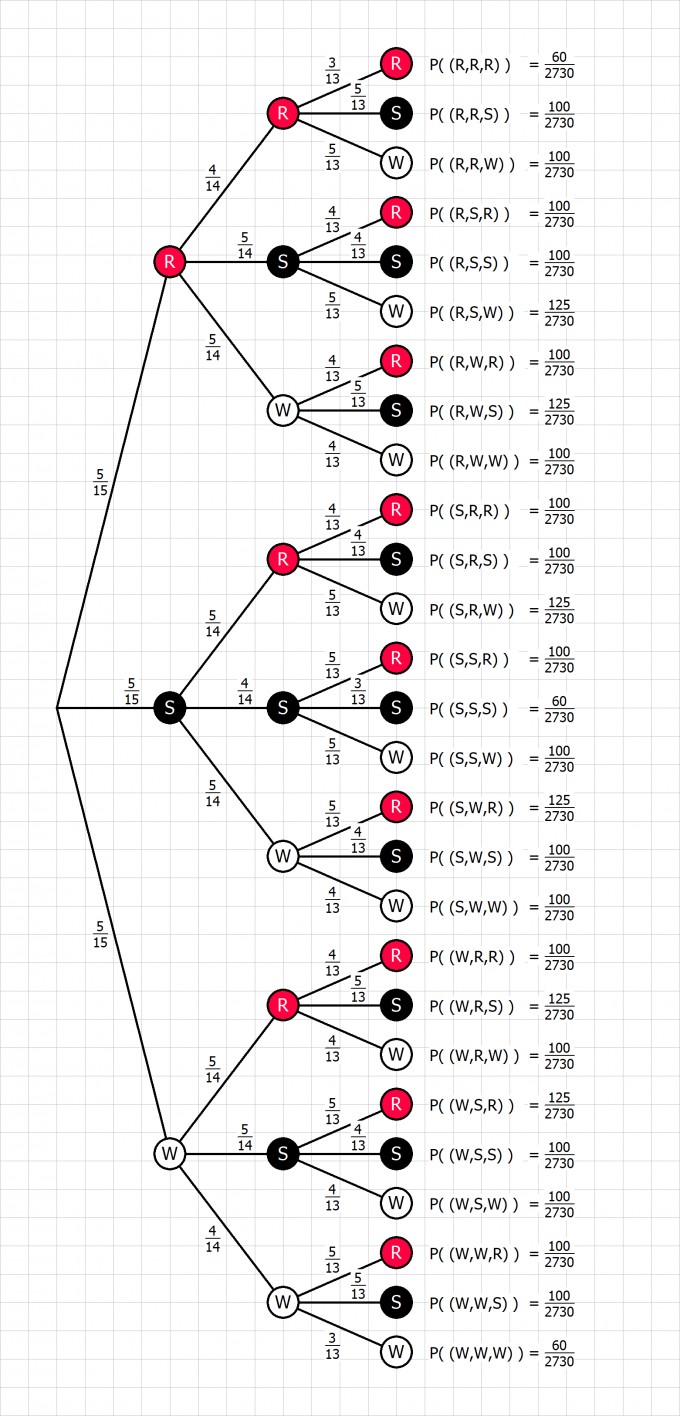
Eine Urne enthält fünf rote, fünf schwarze und fünf weiße Kugeln. Drei Kugeln werden zufällig ohne Zurücklegen gezogen. Wie groß ist die Wahrscheinlichkeit, dass genau zwei verschiedene Farben unter den gezogenen Kugeln vorkommen?
Subtraktiv
P(Genau 2 Farben) = 1 - P(Genau 1 Farbe) - P(3 Farben)
P(Genau 2 Farben) = 1 - (3 * 5/15*4/14*3/13) - (3! * 5/15*5/14*5/13) = 60/91 = 0.6593
Additiv
P({R,R,S}, {R,R,W}, {S,S,R}, {S,S,W}, {W,W,R}, {W,W,S}) = 3 * 3 * 2 * 5/15 * 4/14 * 5/13 = 60/91 = 0.6593
Baumdiagramm ist zwar etwas umfangreich aber durchaus noch machbar.