Schon 2012 formulierten die Didaktiker Walcher und Wittmann:
„Es ist an der Zeit, gründlich darüber zu diskutieren, was fachdidaktisches Wissen ausmacht, in welchem Bezug es zur Fachwissenschaft steht und welche Qualifikationen eine Fachdidaktikerin oder ein Fachdidaktiker haben muss, um dieses fachdidaktische Wissen mathematisch fundiert entwickeln und vermitteln zu können.“
Fachdidaktiker/innen bilden Lehrerinnen und Lehrer aus, die ihrerseits dann Schülerinnen und Schülern Bildung vermitteln. Wer Bildung vermitteln will, muss wissen, worin Bildung besteht. Dazu schrieb Dressler 2006:
„Deshalb gehört es zur Bildung, dass sie unterschiedliche Weltzugänge, unterschiedliche Horizonte des Weltverstehens eröffnet, die ... nicht wechselseitig substituierbar sind und auch nicht nach Geltungshierarchien zu ordnen sind: empirische, logisch-rationale, hermeneutische und musisch-ästhetische Weltzugänge mit ihren jeweils unterschiedlichen Potenzialen an Verfügungswissen und Orientierungswissen, mit ihren jeweils eigenen Rationalitätsformen.“
Dahinter steht ein weit gefasster Bildungsbegriff, den schon Humboldts „So viel Welt als möglich“ im Blick hatte.
Diese Forderung steht kurzschlüssigen Funktionalisierungen von Bildungsinhalten und Bildungszielen entgegen, die zurzeit von der OECD propagiert werden und denen die Politik blind folgt.
Im Rahmen dieses weit gefassten Bildungsbegriffes liefert und erfordert Mathematik eine Weise des Weltverstehens, die unverwechselbar und nicht ersetzbar ist und sich in über 4000 Jahren Kulturgeschichte herausgebildet hat.
Mathematikunterricht sollte in jeweils stufengemäßer Weise erlebbar machen, wie mathematische Wissensbildung
geschieht. Dazu gehört ein Wissen um typisch mathematische Denkhandlungen und die Art ihres Einsatzes. Beispiele für solche Denkhandlungen sind: Darstellen und Wechsel zwischen Darstellungen, Zurückführen von neuem auf Bekanntes, Muster erkennen und in der Sprache der Mathematik beschreiben, Entwickeln (abstrahieren) von Begriffen (auch Zeichen) und Einbau der Begriffe (Zeichen) in weiterführende Gedanken und Begriffsentwicklungen, Begründen und Beweisen.
Selbstverständlich gehören auch Anwendungen zum Mathematikunterricht und mit Sicherheit sollte in der alltagspraktischen Bewältigung des Faches und das hierfür notwendige Verfügungswissen (z. B. Prozentrechnung) vermittelt werden. Wittmann gibt allerdings zu bedenken:
„Effektive Anwendungen der Mathematik beruhen auf innermathematischen Strukturen, die in ausreichendem Maße für sich gewürdigt und entwickelt werden müssen, da sie die unentbehrlichen Bausteine für Modellierungen bilden. Ohne mathematische Theorien gibt es keine effektiven Anwendungen.“
Und weiter:
„Ein gutes Beispiel für eine Fehleinschätzung, zu der man gelangt, wenn man den Blick nur auf die unmittelbaren Anwendungen lenkt, ist die Bruchrechnung. Lebenspraktisch ist sie nur von geringer Bedeutung, aber aus theoretischen Gründen unverzichtbar. Ohne Bruchrechnung hängt insbesondere die Algebra in der Luft, die für Anwendungen von überragender Bedeutung ist.“
In einem vorangegangenen Wissensartikel hatte ich betont, wie wichtig das Erleben mathematischen Wissensgewinns für die Freude an der Mathematik sein kann. Um mathematischen Wissensgewinn Schülerinnen und Schülern erlebbar zu machen, sollten ihnen Aufgaben angeboten werden, bei denen etwas zu entdecken gibt. Ein solches Angebot heute noch zu realisieren ist deshalb schwierig, weil es nur noch um die Anwendung von Mathematik geht. Klassische Themen, die einen Rahmen für Entdeckungen bieten konnten wurden aus den Stoffplänen gestrichen. Dazu gehört auch das Thema ‚geometrische Folgen‘ das vor 20 Jahren noch zum einführenden Stoff der Infinitesimalrechnung gehörte. Innerhalb dieses Themas konnte man Schülerinnen und Schülern folgende, für Entdeckungen gut geeignete Aufgabe stellen:
Ein DIN-A-4-Blatt ABUV wird durch Falten in ein Quadrat und ein Rechteck ABCD zerlegt.
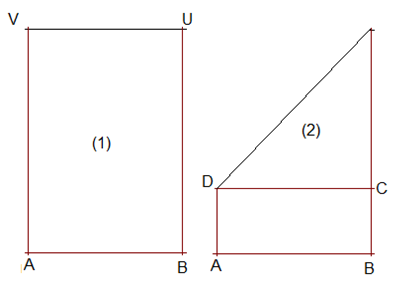
Das Rechteck ABCD wird dann durch Falten in zwei Quadrate und ein Rechteck EFGH zerlegt:
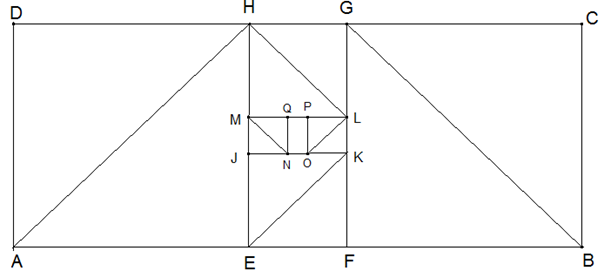
Schneide die Quadrate ab und falte F auf J und G auf M (wie abgebildet). Schneide die Quadrate EFKJ und MLGH ab und erhalte das Rechteck JKLM. Falte K auf P und J auf U (wie abgebildet). Schneide die Quadrate JNQM und QKLP ab und erhalte das Rechteck NOPQ. Führe dieses Vorgehen in Gedanken immer weiter aus.
Schülerinnen und Schülern stellen sich selbsttätig folgende Fragen:
1. Wie oft können solche Faltungen durchgeführt werden?
2. Welche Gesetzmäßigkeiten hinsichtlich der Seitenlängen oder der Flächengrößen der Folge von Rechtecken können gegebenenfalls nachgewiesen werden?
Wie schon betont, basiert Entdecken auf Wissen. In einer Vorstrukturierung müssen die Schülerinnen und Schüler erfahren,
- wie DIN-Formate festgelegt werden,
- was Ähnlichkeit ist,
- was zentrische Streckung/Stauchung ist.
Wenn zusätzlich die Begriffe ‚euklidischer Algorithmus‘, ‚kommensurabel‘, ‚irrational‘ und ‚geometrische Folge‘ innerhalb der Vorstrukturierung behandelt wurden, vergrößert sich das Entdeckungspotential der Aufgabe. In einer nur auf Nutzen und Anwendbarkeit ausgerichteten Mathematik hat die Aufgabe allerdings keinen Platz.
Quellen:
- Dressler, B. (2006): Unterscheidungen. Leipzig: Evangelische Verlagsanstalt.
- Hefendehl-Hebeker, L. (2013): Doppelte Diskontinuität oder die Chance der Brückenschläge. In: Ableitinger, Ch., Kramer, J. & Prediger, S. (Hrsg.): Zur doppelten Diskontinuität in der Gymnasiallehrerbildung. Wiesbaden: Springer,1-15.
- Schwank, I. (1996): Zur Konzeption prädikativer versus kognitiver Strukturen und ihrer Anwendung. In: ZDM-Analysenheft ”Deutsche psychologische Forschung in der Mathematikdidaktik”. Zentralblatt für Didaktik der Mathematik, Vol. 6, 168-183.
- Walcher, S. & Wittmann, E. Ch. (2012): »Minus mal minus« Zum Fundament der COACTIV-Studie. In: MNU 65/6 (1.9.2012), 371-377
- http://schule-intakt.de/wp-content/uploads/2014/08/Schule-intakt-2014-08-04.pdf