Aufgabe:
Die Aufgabenstellung steht im Titel, es steht noch da, dass die Fläche A gegeben ist. Es handelt sich um einen trapezförmigen Querschnitt.
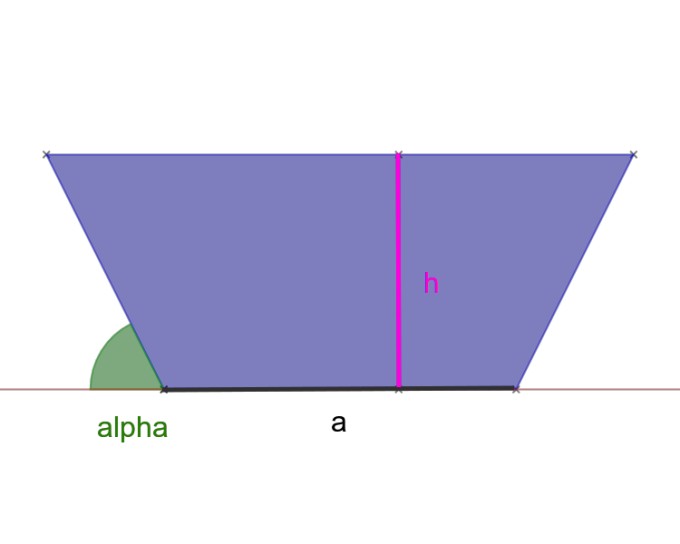
Problem/Ansatz:
Mein Ansatz wäre der, dass ich eine Funktion f finde, die a, h und α als Parameter besitzt, also f(a,h,α): ℝ³→ℝ.
f soll auf den benetzten Umfang abbilden, also f(a,h,α) = 2b + a:
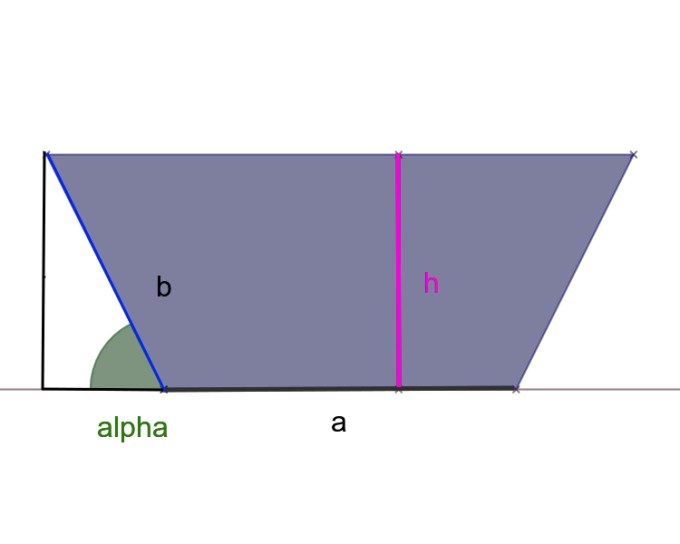
Jetzt würde ich die Form für b aufstellen:
sinα = \( \frac{h}{b} \), b = \( \frac{h}{sinα} \).
Daraus würde dann folgen f(a,h,α) = a + \( \frac{2h}{sinα} \).
Da fehlt mir aber irgendwie noch das gegebene A bzw. der Bezug zum Flächeninhalt im Allgemeinen und wenn ich die partiellen Ableitungen von f bilde und da nach Extremstellen gucke, sieht's auch eher mau aus..
Mein Ansatz war dann, mit den gegebenen Variablen a,h,α die Formel für den Flächinhalt zu bilden:
A = \( \frac{1}{2} \) (a+c) * h. Daraus würde dann werden mit c = \( \frac{2h * sin(90-α)}{sinα} \) + a:
A = \( \frac{1}{2} \) (a+c) * h = \( \frac{1}{2} \) (a+( \( \frac{2h * sin(90-α)}{sinα} \) + a)) * h
= ah + \( \frac{h^{2}sin(90-α)}{sinα} \).
Und dann das in der Funktion zu verwenden, wie f(a,h,α) = \( \frac{a + \frac{2h}{sinα}}{A} \), damit dann auch das A da mit einbezogen wird und man den Wert der benetzten Oberfläche abhängig vom gegebenen A macht....
Würde mich über jegliche Denkanstöße freuen!!