Aufgabe:
Sei \( f : \mathbb{R}^{2} \rightarrow \mathbb{R} \) stetig und in der zweiten Variablen Lipschitz-stetig. Seien \( x_{1}, x_{2} : ] a, b[\rightarrow \mathbb{R} \) zwei Lösungen der Differentialgleichung \( x^{\prime}=f(t, x) \).
Zeigen Sie: Wenn es \( t_{1}, t_{2} \in ] a, b[ \) mit \( x_{1}\left(t_{1}\right) \leq x_{2}\left(t_{1}\right) \) und \( x_{1}\left(t_{2}\right) \geq x_{2}\left(t_{2}\right) \) gibt, dann gilt \( x_{1}(t)=x_{2}(t) \) für alle \( t \in ] a, b[ \).
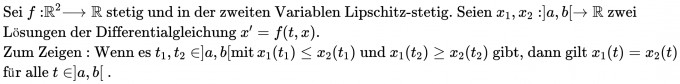
Wie geht man bei solche. Aufgaben allgemein vor? Könnte mir das einer Schritt für Schritt erklären was gemacht werden muss?