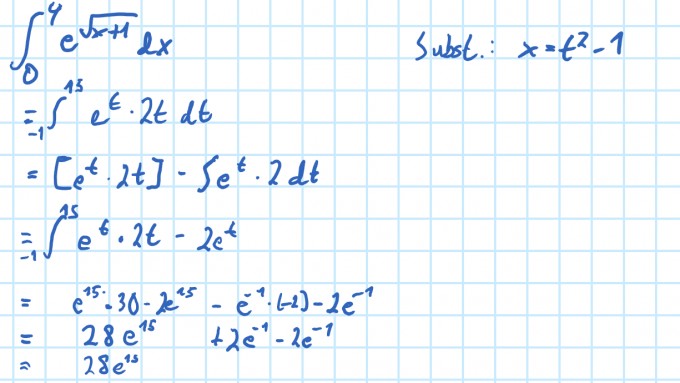Aufgabe zu Integralrechnung

Question

Aufgabe:

Ich soll bestimmt Integralle berechnen und komme bei diesen 2 nicht weiter:

1)₀∫⁴ e^√x+1 dx (mit Substitution x := t² − 1)

ich hoffe man erkennt : e hoch wurzel x+1.

2) _-1∫¹ sin(x)/(1+x⁴) dx

Problem/Ansatz:

für 1) siehe Bild, die Lösung ist aber anscheinend nicht richtig....  für 2) habe ich gar keine Idee

Comments

Bei (2) gibt's nicht viel zu rechnen. Es braucht keine Stammfunktion.

---

Das heißt ich soll einfach nur die Werte des Integrals in x einsetzen ohne irgendwas sonst zu tun?

Answer 1

Aufgabe 2) Der Wert des Integrales ist 0.(aufgrund der Symmetrie)

Aufgabe 1)

Comments

Wow, vielen Dank!

Meine Idee war wohl nicht so schlecht, bloß schlecht umgesetzt :)

Answer 2

Die obere Integrationsgrenze muss √3 heißen.

Comments

Wieso? Wäre aber trotzdem ein anderes Ergebnis als bei Wolfram Alpha.

---

Auch die Grenzen müssen durch die gleiche Substitution umgerechnet werden:

0= t² − 1, t=±1

4= t² − 1, t=±√5 (war bei mir falsch)

Answer 3

bei (2) der Wert des Integrales ist 0.
Sei : 

\( f(x)=\frac{sin(x)}{1+x^{4}} \) dann gilt f(-x)=-f(x)

Da der integral von -1 bis 1 ist, ist der Wert einfach 0

~plot~ sin(x)/(1+x^4);x=1;x=-1; ~plot~