Moin
Aufgabe:
Für welche Werte des Parameters t ∈ R besitzt das lineare Gleichungssystem
x + y + tz = −1
3x + (t + 1)y + (t − 1)z = −1
tx + 2y + z = 0
a) genau eine Lösung
b) unendlich viele Lösungen oder
c) gar keine Lösung?
Problem/Ansatz:
BIn zwar soweit gekommen aber, aber auf die vorgegebene Lösung komme ich leider nicht:
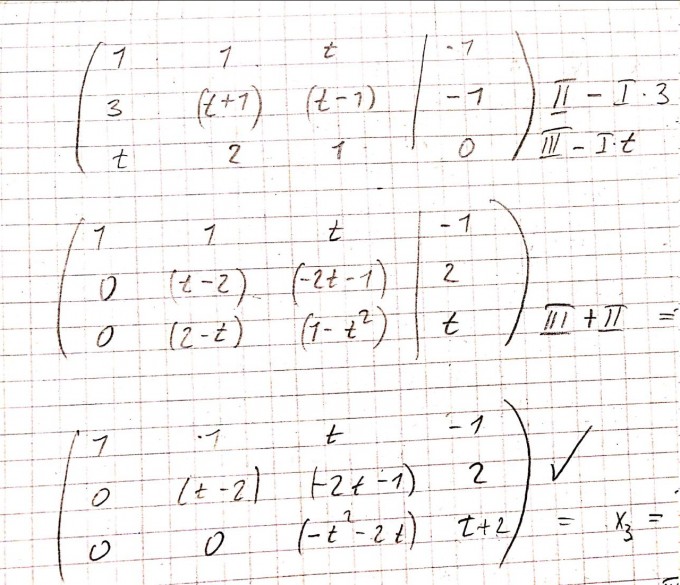
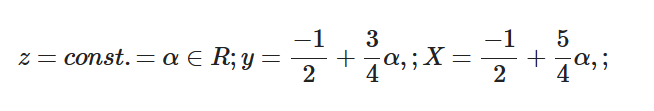
Für t ungleich {−2, 0, 2} ist die eindeutige Lösung
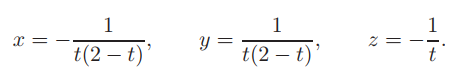
Ich hoffe einer kann mir weiterhelfen.
Vielen Dank im Voraus
GK