Halbierung einer Dreiecksfläche

Question

Vom inneren Punkt P eines Dreiecks ABC werden die drei Verbindungsstrecken zu den Eckpunkten gezeichnet. Außerdem werden die Strecken PE, PD und PF jeweils parallel zu einer Seitenhalbierenden von ABC gezeichnet. Zeige, dass die grau unterlegten Flächen die halbe Dreiecksfläche bedecken.

Comments

Vom Duplikat:

Titel: Halbierung einer Dreiecksfläche

Stichworte: dreieck,flächenstück

Vom inneren Punkt P eines Dreiecks ABC werden die drei Verbindungsstrecken zu den Eckpunkten gezeichnet. Außerdem werden die Strecken PE, PD und PF jeweils parallel zu einer Seitenhalbierenden von ABC gezeichnet. Zeige, dass die grau unterlegten Flächen die halbe Dreiecksfläche bedecken.

---

Du meinst mit "Seitenhalbierenden" "Schwerlinien", oder?

https://de.wikipedia.org/wiki/Seitenhalbierende

Mir gefällt dieser Begriff nicht wirklich, da man ihn mit den Mittelsenkrechten verwechseln kann.

---

Dein Link nennt "Seitenhalbierende" und "Schwerlinien" als Synonyme. Aber schön, dass du die Aufgabe wohl angehen möchtest.

---

Hallo

ich löse Puzzles um jemand zu helfen, nicht so gern als Versuchsobjekt dafür, wie leicht oder schwer eine Frage ist. Kannst du also bitte sagen, ob du die Antwort kennst, oder es eine echte Frage ist. Wenn echt: soll es elementargeometrisch, mit Abbildungsgesetzen oder Vektorgeometrie usw. gelöst werden?

Gruß lul

---

Wenn du die Aufgabe nicht lösen willst, kann dich niemand dazu zwingen. Hier in Forum "mathelounge" ist alles freiwillig. Die Aufgabe ist elementargeometrisch lösbar. Ich warte eigentlich auf eine Antwort des superklugen Gast hj2166.

---

Hallo

 natürlich muss ich nicht antworten, trotzdem ist die Frage berechtigt, ob du die Antwort, bzw. eine Antwort kennst oder nicht.

Gruß lul

---

Mindestens weiß ich, dass die Aufgabe elementargeometrisch lösbar ist und zwar mit Hilfe dreier Hilfslinien.

---

"oder" steht auch erst nach den beiden Synonymen in meinem Link.

---

Bei dieser Aufgabe geht es um Diagonalen in Parallelogrammen, um die Ähnlichkeit von Dreiecken und um deren Seitenhalbierende.

Was verstehst du daran nicht ?

---

Ist der Satz von Ceva nicht anwendbar?

---

@rc: Weitere Fragen (und allenfalls Duplikate) von Roland findest du hier https://www.mathelounge.de/user/Roland/questions

---

Danke, ich habe es irgendwie nicht mehr gefunden. Gasthj, möchtest du vielleicht deine Ideen weiter ausführen? Ich hatte einen anderen Ansatz gewählt, prüfe allerdings noch auf Makellosigkeit.

---

Gasthj, möchtest du vielleicht deine Ideen weiter ausführen? Ich hatte einen anderen Ansatz gewählt

Du hast doch ganz genau den von mir skizzierten Entwurf verfolgt und durchgeführt., also keinen anderen Ansatz.
Und natürlich hast du dabei den Satz von Ceva benutzt.

---

Ich habe viel herumexperimentiert, um auf die Lösung zu kommen. Kribbelt es dir nicht in den Fingern, wenn du einen Beweis gefunden hast, diesen auch zu teilen? Vielleicht hast du ja auch schon alle Milleniumprobleme an einem Nachmittag gelöst und verwahrst sie im Keller oder schreibst sie gar nicht auf wie Fermat.

---

Ich wollte wissen, ob Rs Kommentar   Ich warte eigentlich auf eine Antwort des superklugen Gast hj2166.   reine Provokation war oder ob es ihm wirklich um die Aufklärung eines für ihn unlösbaren Problems ging.
Leider hat er auf meine Frage nicht reagiert.

---

Zweiteres und ich denke, dass das als Kompliment gemeint war.

Answer 1

Hallo Roland,

mit Hilfe tatkräftiger Mathematiker, kann ich dir nun einen Beweis präsentieren:

Beweis:

Seien  $\{F_1,F_2\}\subset AC$, $\{E_1,E_2\}\subset BC$ und $\{D_1,D_2\}\subset AB$, so dass $F_1E_2||AB$,  $D_2E_1||AC$,  $D_1F_2||BC$ und $F_1E_2\cap D_2E_1\cap D_1F_2=\{P\}.$

Weiterhin, wegen:$$\Delta PE_2E_1\sim\Delta F_1PF_2\sim\Delta D_2D_1P\sim\Delta ABC,$$ können wir schlussfolgern, dass $PE$, $PF$ und $PD$ die Seitenhalbierenden von jeweils $\Delta PE_1E_2,$, $\Delta PF_1F_2$ und $\Delta PD_1D_2$ sind.

Darüber hinaus, da $AF_1PD_2$,  $BD_1PE_2$ und $CE_1PF_2$ Parallelogramme sind, erhalten wir insgesamt:$$S_{\Delta PAD}+S_{\Delta PBE}+S_{\Delta PCF}$$$$=\left(S_{\Delta PAF_1}+S_{\Delta PDD_1}\right)+\left(S_{\Delta PBD_1}+S_{\Delta PEE_1}\right)+\left(S_{\Delta PCE_1}+S_{\Delta PFF_1}\right)$$$$=\left(S_{\Delta PAF_1}+S_{\Delta PFF_1}\right)+\left(S_{\Delta PBD_1}+S_{\Delta PDD_1}\right)+\left(S_{\Delta PCE_1}+S_{\Delta PEE_1}\right)$$$$=S_{\Delta PAF}+S_{\Delta PBD}+S_{\Delta PCE}$$

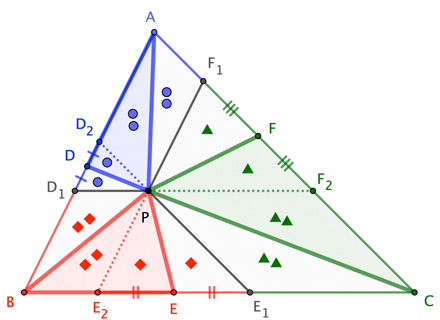
Skizze:

Comments

Vielen lieben Dank für die Mühe. Auch von mir einen Daumen.