wie kann man mathematisch betrachtet begründen, dass 2x^-3 nicht "null wird" bzw. keine wendepunkt hat obwohl es eine rechts und linkskrümmung hat die funktion?
2 * x^-3 = 2 / x^3
Damit der Ausdruck 0 wird muß der Zähler null
werden. Das ist er aber nicht.
2 / x^3 > 0
x muß positiv sein, dann stimmts
Linkskrümmung
2 / x^3 < 0
x muß negativ sein, dann stimmts
Rechtskrümmung
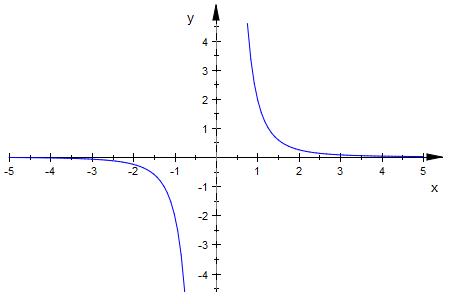
Krümmung ist null : gibt es nicht