Analytische Geometrie mit Vektoren: Lehrsatz beweisen. Könnte mir jemand weiter helfen?

Question

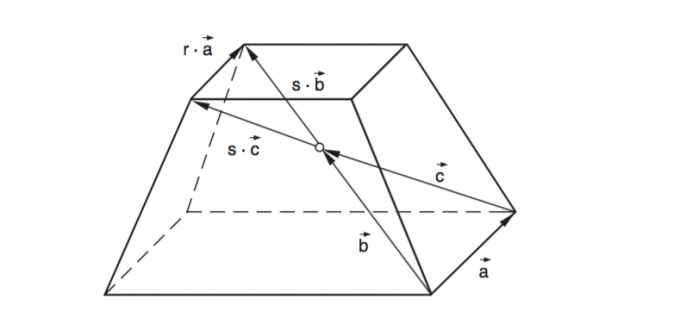
Beweisen Sie den Lehrsatz: In einem geraden Pyramidenstumpf (Siehe Abb.) mit rechteckigen Grund- und Deckfläche werden die Raumdiagonalen von ihrem gemeinsamen Schnittpunkt in demselben Verhältnis geteilt, in dem die entsprechende Seiten der Grund- und Deckfläche stehen.

Meine Ideen:

Ich habe andere fragen auf dieser Aufgabe im Internet gefunden.. ich habe mitgenommen:

\( \vec{a} \) + \( \vec{c} \) + s\( \vec{c} \) + r\( \vec{a} \) – s\( \vec{b} \) – \( \vec{b} \) = 0

⇔ \( \vec{a} \)(1 + r) + \( \vec{b} \)(–1 – s) + \( \vec{c} \)(1 + s) = 0

Man erkennt \( \vec{c} \) = \( \vec{b} \) – \( \vec{a} \). Einsetzen:

\( \vec{a} \)(1 + r) + \( \vec{b} \)(–1 – s) + ([\( \vec{b} \) – \( \vec{a} \)]*[1 + s]) = 0

⇔\( \vec{a} \)(1 + r) + \( \vec{b} \)(–1 – s) – \( \vec{b} \) – s\( \vec{b} \) + \( \vec{a} \) + s\( \vec{a} \) = 0

⇔ \( \vec{a} \)(2 + r + s) + \( \vec{b} \)(–2 – 2s) = 0

Und jetzt weiß ich leider nicht weiter... :(

Könnte mir jemand bitte weiter helfen? Was mache ich jetzt?

Answer 1

Ich habe deine Herleitung übersprungen und nur die letzte Zeile angesehen. (Ob deine Zwischenschritte richtig oder falsch sind mögen andere beurteilen).

Du schreibst am Ende

"Vielfaches von Vektor a plus Vielfaches vom Vektor b = 0".

Das ist schon mal prinzipiell falsch. Die Summe der Vielfachen mehrerer Vektoren ist keine Zahl, sondern wieder ein Vektor.

Möglicherweise meinst du

"Vielfaches von Vektor a plus Vielfaches vom Vektor b = Nullvektor".

Da die Vektoren a und b in verschiedene Richtungen zeigen, kann da nur unter einer Bedingung der Nullvektor rauskommen: die beiden Faktoren vor den Vektoren a und b sind beide Null.

Das ergäbe ein (lösbares) Gleichungssystem.

Ich verstehe allerdings nicht, warum man hier ohne Not die Vektorrechnung bemüht. Der Beweis funktioniert mit Mitteln der Klasse 8 (Stichwort: Strahlensatz).

PS: Jetzt habe ich doch auch mal deine vorletzte Zeile angesehen und dort am Ende mehrere falsche Vorzeichen festgestellt. Schau da nochmal drüber.

Comments

Vielen Dank für Ihre Hilfe!! Ich werde die vorzeichenfehler korrigieren und erneut abschreiben mit " = \( \vec{0} \) ". Wäre das dann eine ausreichende Antwort zu meine Aufgabe?

Answer 2

Du hast im vorletzten Schritt einen Vorzeichenfehler:

$$\Leftrightarrow\vec{a}(1+r)+\vec{b}(-1-s)+\vec{b}+\vec{b}s-\vec{a}-\vec{a}s=\vec{0}\\\Leftrightarrow\vec{a}r-\vec{a}s=\vec{0}\\\Leftrightarrow r=s$$

Gruß Woodoo

Comments

Vielen vielen Dank für die Korrektur! Wär dies eine ausreichende Antwort zur Aufgabe?

---

Du sollst zeigen, dass die Verhältnisse gleich sind. Das haben wir doch gemacht, oder?

Ich finde, das passt!!!

---

Yay! Dankeee :D