Ganzrationale Funktion 3.Grades aufstellen. Wie lautet die Funktionsgleichung?

Question

Nachtrag: Genaue Aufgabe im Bild im Kommentar:

Wir müssen eine ganzrationale Funktion 3.Grades aufstellen, die folgende Kriterien beinhaltet:

Wendepunkt  W(1/-1)

Eine einfache Nullstelle bei f(-1)

Keine Symmetrie

ungerader, negativer Exponent (3) aufgrund des Globalverlaufs

Problem/Ansatz:

f(x)= -a^2*(x+1)

Comments

Kannst du die Aufgabe bitte so mitteilen, wie sie gestellt wurde?

---

Das habe ich bereits.

---

Ok, dann verstehe ich die Zeile "ungerader, negativer Exponent (3) aufgrund des Globalverlaufs" nicht. Wo kommt das her?

---

Und "Eine einfache Nullstelle bei f(-1)" ist auch nicht sinnvoll.

---

Daß ist deren Graph und nun ist nach der Funktionsgleichung gefragt.

---

Ok, damit ist dein Ansatz allerdings nicht richtig. Es ergeben sich die Bedingungen

(1) f(-1)=0 (Nullstelle x=-1)

und wegen des Sattelpunktes (1|-1) noch

(2) f(1)=-1

(3) f'(1)=0 und

(4) f''(1)=0.

---

Das ist aber nur deine Privatmeinung.

Answer 1

ungerader, negativer Exponent (3) aufgrund des Globalverlaufs

Steht sicher nicht so in der Fragestellung (sollte das jedenfalls nicht).

Fragestellung ist unvollständig / unverstanden gestellt. Bei ganzrationalen Funktionen kommen keine negativen Exponenten vor.

Zudem:

f(x)= -a^2*(x+1)

? Woher kommt das denn?

Comments

Ich meinte negativer Koeffizient.

---

Dein Ansatz führt nicht auf eine Funktion dritten Grades.

f(x)= -a^2*(x+1)

Zudem: Was bringt es, wenn du a quadrierst?

---

@Nachgelieferte Skizze: Beginne mal mit g(x) = -x^3 Nun stauchen und dann noch verschieben.

Vielleicht so ~plot~ -x^3;-0.125x^3;(x-1)^3*(-0.125)-1 ~plot~

---

D.h. du brauchst auch hier kein Gleichungssystem aufzustellen und zu lösen.

Answer 2

Nach dem von dir eingestellten Graphen ist
f(-1)=0 ( Nullstelle )
f(1)=-1 ( Koordinaten )
f'(1)=0  ( Steigung )
f''(1)=0  ( Krümmung )

Zur Kontrolle
f(x) = -0,125·x^3 + 0,375·x^2 - 0,375·x - 0,875

Falls du den Rechenweg erklärt haben willst
dann melde dich.
Du sollst nicht unwissend sterben.

Comments

Oder vielleicht so :

~plot~ (-1.06*x^3+3.18*x^2-2.94*x-7.18)/8 ~plot~

Answer 3

Ich empfehle bei Steckbriefaufgaben zur Selbstkontrolle

http://www.arndt-bruenner.de/mathe/scripts/steckbrief.htm

Dort kann man dann auch schnell seine vermuteten Bedingungen reinschreiben und schauen was der Rechner daraus macht. So entwickelt man leicht ein Gefühl wie man vorgehen kann.

Leichter ist es hier eine punktsymmetrische Funktion im Ursprung aufzustellen und diese dann zu verschieben. Da braucht man nichts rechnen.

f(x) = - 1/2^3·(x - 1)^3 - 1

Answer 4

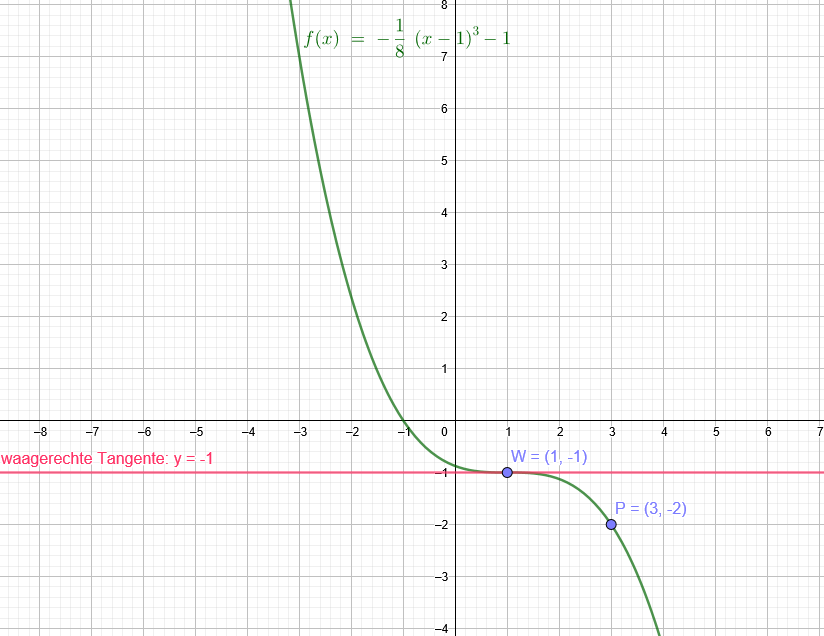
Wendepunkt W(1|-1) und P(3|-2)

Ich verschiebe den Graph der Funktion um eine Einheit nach oben:

Wendepunkt W(1|0) und P(3|-1)

Im Wendepunkt ist eine dreifache Nullstelle.

Nullstellenform der Parabel 3.Grades:

p(x)=a*(x-1)^3

p(3)=a*(3-1)^3 = 8a

8a =  - 1

a=  -  \( \frac{1}{8} \)  

p(x)  =  -\( \frac{1}{8} \)  *(x-1)^3

Wieder eine Einheit nach unten:

f(x)  =  - \( \frac{1}{8} \)   * (  x - 1 ) ^3 -1

mfG

Moliets