Hallo Ben,
als ich die Frage gelesen hatte, hätte ich intuitiv geantwortet, dass Translation und Skalierung natürlich nicht kommutativ sind. Nun hat aber Tschakabumba 'bewiesen', dass das doch kommunativ ist. Allerdings enthält dieser Beweis IMHO einen Fehler. Die Skalierungsmatrix \(S\) ist meiner Meinung nach
$$S = \begin{pmatrix} \lambda & 0 & 0 \\ 0 & \lambda & 0 \\ 0& 0& \colorbox{#ffff00}{1} \end{pmatrix}$$
D.h. rechts unten steht eine \(1\) und nicht der Faktor \(\lambda\) der Skalierung. Eine einfache Matrizenmultiplikation zeigt dann sofort, dass man zwei verschiedene Ergebnisse erhält, wenn man Translation und Skalierung vertauscht. Also nicht kommutativ.
Zur Anschauung habe ich das mal als 3D-Szene dargestellt.
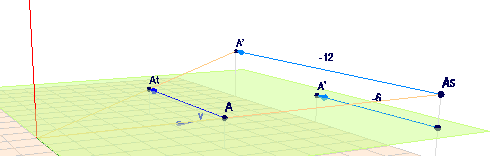
(klick bitte auf das Bild, dann öffnet sich eine 3D-Ansicht)
Dort siehst Du den Punkt \(A=(4|\,5|\,1)\), der in der grünen Ebene liegt. Diese Ebene liegt bei \(z=1\) und wenn das Thema Computergraphik ist, dann kann das die Ebene sein, die der Bildschirm der Computers anzeigt - der ist ja nur 2-dimensional. Nach einer Translation um \(-6\) in \(X\)-Richtung befindet sich das Bild des Punktes bei \(A_t = (-2|\,5|\,1)\). Nach einer Skalierung von \(A\) würde er sich bei \(A_s=(8|\,10|\,\colorbox{#ff8888}{2})\) befinden, wenn man die die Matrix von Tschakabumba anwendet
WIe bekommst Du \(A_s\) aber wieder in die grüne Ebene - d.h. auf den Bildschirm? Das (mir bekannte) klassische Vorgehen besteht darin, alle Koordinaten des Vektors durch die z-Koordinate zu dividieren, so dass die z-Koordinate wieder zu 1 wird. Das bringt uns aber nur wieder zurück zu \(A\) und \(A_s\) würde sich von von seinem skalierten Bild nicht unterscheiden - das kann es als nicht sein. Ok - vergessen wir einfach mal die z-Koordinate und zeichnen \(A_s\) bei \((8|\,10)\). Scheinbar alles gut, aber was passiert bei einer anschließenden Translation, die doch die gleiche sein soll wie die von \(A=(4|\, 5)\) nach \((-2|\, 5)\)?
Es soll doch nur um \(-6\) in X-Richtung verschoben werden, aber Du landest um ganze 12 Einheiten von ursprünglichen Punkt entfernt .. wolltest Du das?
Noch ein Anwendungsfall: Skaliere den Punkt \(A\) um den Faktor 2. Füge dann einen weiteren Punkt \(B=(8|6)\) hinzu (welchen Wert hat die z-Kooridnate von \(B\)?) und führe anschließend für beide Punkte die gleiche Translation durch, die Punkt \(A\) nach \(A_t=(-2|\,5)\) gebracht hätte. Zeichne dir das ganze einfach mal auf und rechne es nach.
Nachtrag:
man könnte das aber auch anders sehen. Gefragt ist doch 'Geben Sie eine Translationsmatrix an, die einen Punkt (4,5) in den Punkt (-2,5) verschiebt' ohne genau zu definieren was mit 'Translation' gemeint ist. Also könnte man doch eine Scherung annehmen mit $$T = \begin{pmatrix} 1& -\frac 65 \\ 0& 1 \end{pmatrix}$$ Und es gilt wie gefordert:$$\begin{pmatrix} -2 \\ 5 \end{pmatrix} = T \cdot \begin{pmatrix} 4 \\ 5 \end{pmatrix}$$ ganz ohne homogene Koordinaten und demnach ist \(S\) einfach$$S = \begin{pmatrix} \lambda& 0\\ 0& \lambda \end{pmatrix} $$ Und es gilt allgemein $$T \cdot S = S \cdot T$$genau aus den Gründen, die Tschakabumba bereits dargelegt hat.
Gruß Werner