Da du keine wirklich genauen (oder richtigen) Angaben gemacht hast, kann ich dir nur eine Antwort auf Basis von meinen Annahmen geben.
Annahme:
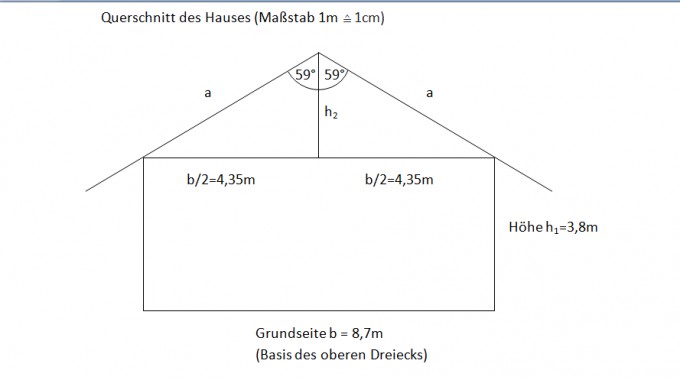
Es handelt sich um eine quadratische Grundfläche mit einer Grundseite der Länge 8,7m.
Die Höhe des Hauses h1 ohne Dach beträgt 3,8m.
Das Dach des Hauses hat den Querschnitt eines gleichschenkligen Dreiecks, wobei der Winkel zwischen den Schenkeln 118° beträgt.
Antwort:
Der dreieckige Querschnitt hat eine Basis b der Länge 8,7m (Grundseitenlänge). Der gegenüberliegende Winkel beträgt 118°. Die Schenkellänge a berechnet sich mit $$a=\frac{b}{2*sin(59°)}=\frac{8,7m}{2*sin(59°)}≈ 5,075m$$Nach Satz des Pythagoras ist die Höhe des Daches$$h_2=\sqrt{a^2-(\frac{b}{2}})^2=\sqrt{(5,075m)^2-(\frac{8,7m}{2}})^2≈ 2,614m$$
Somit ist die Gesamthöhe des Hauses $$h=h_1+h_2≈ 3,8m+2,614m=6,414m$$