Y Wert einer Parabel ohne Funktionsgleichung

Question

Aufgabe:

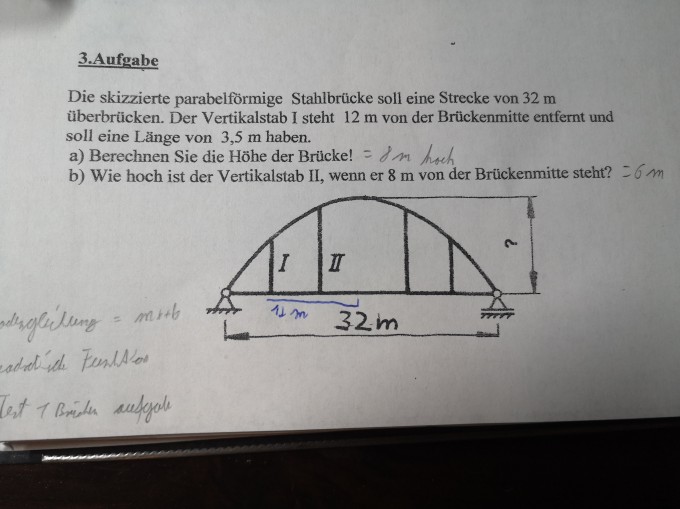
Die skizzierte prabelförmige l Stahlbrücke soll eine Strecke von 32 m überbrücken. Der Vertikalstab I steht 12 m von der Brückenmitte entfernt und soll eine Länge von 3,5m haben.

a) Berechnen sie die Höhe der Brücke!

b)Wie hoch ist der Vertikalstab II,wenn er 8m von der Brückenmitte entfernt steht?

Problem/Ansatz:

Ich bin bei Aufgabe a) und hab die Nullstellen Schreibweise

verwendet y=f(x)=a(x-0)•(x-32) jetzt weiß ich nicht wie jetzt die Höhe der Brücke(8m) berechnen werden kann.

Grüße,

Answer 1

Aloha :)

Dein Ansatz ist völlig richtig: \(y=ax(x-32)\).

Zur Bestimmung von \(a\) kannst du die Information "Der Vertikalstab I steht 12m von der Brückenmitte entfernt und soll eine Länge von 3,5m haben." nutzen. Die Brückenmitte ist aus Symmetriegründen bei \(x=16\). Der Vertikalstab steht \(12m\) links davon, also bei \(x=4\), und seine Höhe ist \(3,5m\).$$\frac{7}{2}=y(4)=4a\cdot(4-32)=-112a\;\;\Rightarrow\;\;a=-\frac{7}{224}$$Damit ist die Höhe der Brücke$$H=-\frac{7}{224}\cdot16\cdot(16-32)=-\frac{7}{224}\cdot(-256)=8$$

Answer 2

Hallo

1. es ist besser x=0 bei der Mitte anzunehmen.

dann hast du erstmal y=ax^2+b oder y=-ax^2+b

du weisst y(16)=0 und y(12)=3,5

 hast also 2 Gleichungen für a und b und b ist die Höhe.

aber auch mit deinem Ansatz weisst du eigentlich, dass y((16-12)=y(4)=3,5. 12 m von der Mitte ist 4m von x=0 bei dir.

Gruß lul

Comments

Ich finde seinen Produktansatz sehr gut und einleuchtend, weil ja die beiden Nullstellen gegeben sind. Dadurch ist in der Gleichung nur eine Unbekannte \(a\), die schnell bestimmt werden kann.