Aufgabe:
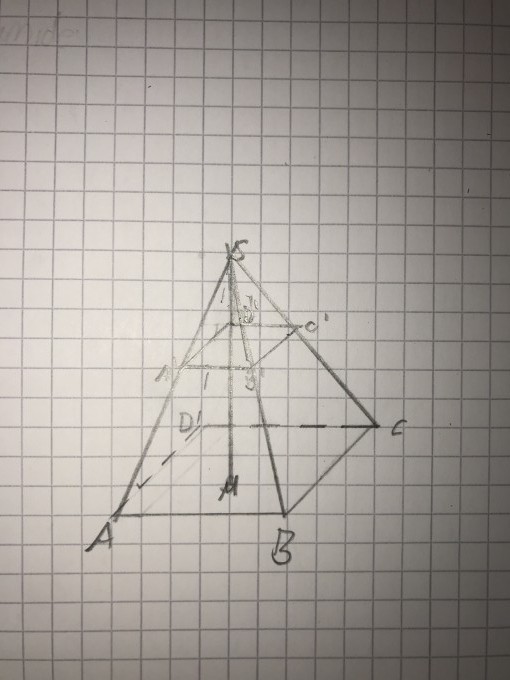
Gegeben ist eine quadratische Pyramide mit den Eckpunkten A(0/0/0), B (0/7/0), C(-7/7/0) und D(-7-7/0) und der Spitze S (-3,5/3,5/19,85). Eine Einheit entspricht 1cm (Zeichnung folgt im Anhang)
a) Geben Sie Gleichungen für die Gerade g durch A und S, h durch A und C und k durch A und B in Parameterform an.
b) Berechnen Sie die Innenwinkel der Dreiecke AMS und ABS.
c) Eine Packung für Frischkäse hat die Form eines Pyramidenstumpfes (Koordinaten der Grundfläche s. Oben). Geben Sie die Koordinaten der Eckpunkte der oberen Fläche an, wenn die Höhe der Käsepackung 17/3 beträgt.
d) Berechnen Sie das Volumen der Frischkäsepackung.
Problem/Ansatz:
a) und b) habe ich bereits gelöst.
a) g: Vektor x= (0/0/0) + r* (-3,5/3,5/19,85)
h: Vektor x= (0/0/0) + s* (-7/7/0)
k: Vektor x= (0/0/0) + t* (0/7/0)
b) Dreieck AMS (rechtwinklig) alpha = 76 Grad; beta = 90 Grad; gamma = 14 Grad
Dreieck ABS (gleichschenklig) alpha = 80,15 Grad; beta = 80,15 Grad, gamma = 19,70 Grad
c) Wiegesagt Zeichnung findet ihr unten. Ich hab schon ein bisschen was recherchiert und probiert aber ich komme da rechnerisch einfach nicht weiter und das was ich so gefunden hatte, die Rechenwege kamen mir nicht bekannt vor, jedenfalls nicht aus dem Unterricht.
d) hier gilt dasselbe im Prinzip. Die Formel kenne ich: V= 1/3 * h * (G1 + (Wurzel aus G1* G2) + G2
G1 und G2 (sofern beides quadratische Grundflächen sind) müsste ich doch über Beträge rauskriegen, sobald ich die oberen Eckpunkte habe oder nicht?
Also fürs erste bräuchte ich ganz e Hilfe bei der c) weil ich da echt nicht weiterweiß und vielleicht jemanden, der mir netterweise sagen könnte, ob meine Heransgehensweise an die d) prinzipiell richtig ist.
Vielen Dank für jede Mithilfe!