hi
a)
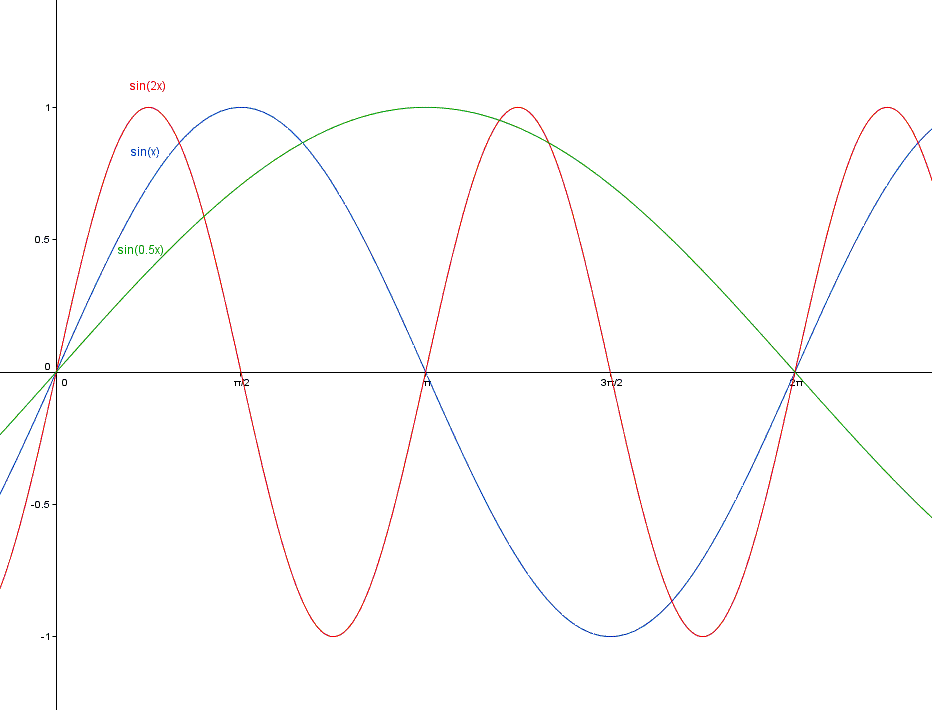
der graph der funktion sin(2x) erscheint im vergleich zum graphen
der funktion sin(x) in x-richtung gestaucht, weil 2x das doppelte funktionsargument von x ist.
angefangen bei x=0, sich entlang der positiven x-ache bewegend
steigen die funktionswerte(y-werte) von sin(2x) aufgrund des doppelten
funktionsarguments schneller an.
demzufolge ereicht die funktion sin(2x) ihr maximum vor der funktion sin(x) und
darum fallen die funktionswerte von sin(2x) auch früher. darum lässt dieser verlauf
sin(2x) gegenüber sin(x) in x-richtung gestaucht erscheinen.
man kann auch mit der anzahl der nullstellen argumentieren.
die funktion sin(x) hat bekanntlich nullstellen bei x = kπ, k ∈ ℤ.
bei welchen werten wird sin(2x) gleich null?
das ist der fall bei 2x = kπ, also bei x = kπ/2.
guckt man sich die anzahl der nullstellen von sin(x) innerhalb von 0 <= x <= 2π an,
so sieht man sie bei 0π, π, 2π.
sin(2x) dagegen hat nullstellen bei 0π, π/2, π, 3π/2, 2π.
offensichtlich hat sin(2x) im intervalls [0, 2π] mehr nullstellen als
sin(x), schneidet also die x-achse in diesem intervall öfter.
das lässt den graphen von sin(2x) in x-richtung gestaucht erscheinen.
b)
der graph von sin(0.5x) sieht gegenüber dem graphen von sin(x) in x-richtung gestreckt aus, weil
0.5x das halbe funktionsargument von x ist. sin(0.5x) erreicht daher die funktionswerte
im vergleich zu sin(x) später, darum fällt sin(0.5x) auch später. das lässt den
graphen von sin(0.5x) in x-richtung gestreckt aussehen.
auch hier kann man mit der anzahl der nullstellen argumentieren.
sin(0.5x) wird null, wenn 0.5x = x/2 = kπ gilt. das ist bei x = 2kπ der fall.
sin(0.5x) hat also innerhalb des intervalls [0, 2π] nullstellen bei 0π und 2π.
das sind deutlich weniger nullstellen als sin(x) hat. darum sieht sin(0.5x) im
vergleich zu sin(x) in x-richtung gestreckt aus.