Höhe und mittlere Geschwindigkeit berechnen

Question

Aufgabe:

Ein Wetterballon steigt senkrecht auf. In 2 km Entfernung vom Startplatz befindet sich ein Beobachtungspunkt auf gleicher Meereshöhe. Von dort aus erscheint der Wetterballon 10 Minuten nach dem Start unter einem Höhenwinkel von 14° und 15 Minuten nach dem Start unter einem Höhenwinkel von 22°.

1.) Welche Höhe hat der Ballon zum ersten Kontrollzeitpunkt nach 10 Minuten erreicht, welche Höhe zum zweiten nach 15 Minuten?

2.) Berechne die mittleren Geschwindigkeiten des Ballons bis zum ersten Kontrollzeitpunkt und zwischen erstem und zweiten Kontrollzeitpunkt.

Problem/Ansatz:

Ich habe Probleme dabei herauszufinden wie ich das jetzt berechnen soll. Eine Erklärung wie ich jetzt vorgehen soll wäre echt toll, mehr verlange ich auch gar nicht, brauche nur eine Erkärung. Und auch mit welchen Werten ich rehnen soll.

Answer 1

Da du dir nur Erklärungen (Ansätze,...) ohne Lösungen gewünscht hast:

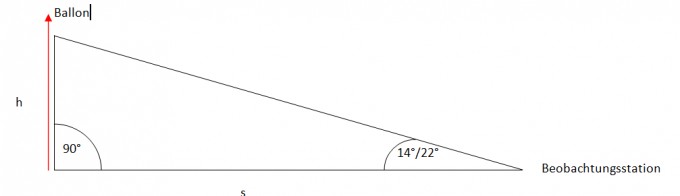
1.) Der Ballon steigt senkrecht auf. Bezeichnen wir die Höhe des Ballons in km als h. In 2 km Entfernung auf gleicher Ebene befindet sich ein Beobachtungspunkt. Bezeichnen wir die Länge der Strecke in km als s mit s=2. Nun sei der Höhenwinkel 14° und 22°.

Ich habe dir eine Skizze für die Lösung mal angehängt.

2.) Mittlere Geschwindigkeit zum ersten Kontrollzeitpunkt:

$$v=\frac{Änderung(Höhe)}{Änderung(t)}=\frac{Höhe_1}{t_1}$$ ,da Anfangshöhe = Anfangszeit = 0. Erster Kontrollzeitpunkt t₁ = 10 min = 1/6 * h. Höhe₁ für den Zeitpunkt kannst du aus 1.) für den Winkel 14° übernehmen.

Mittlere Geschwindigkeit zwischen erstem und zweitem Kontrollzeitpunkt:

$$v=\frac{Änderung(Höhe)}{Änderung(t)}=\frac{Höhe_2-Höhe_1}{t_2-t_1}$$

Höhe₁ siehe vorher, Höhe₂ aus 1.) für 22° Winkel, t₁ siehe vorher, t₂ = 15 min = 1/4 * h

Comments

Vielen Dank!