Graphen sollen sich im Schnittpunkt der Funktionen orthogonal schneiden

Question

gegeben:

f(x)= 8√(x) -14

g(x)= 8/x
a)nachweisen das der Punkt (4 | f(4)) Schnittpunkt beider Funktionen ist

b) Zeigen das f + g orthogonal sind

Ich weiß nicht ob ich es mit Ableitungsfunktion machen muss oder nicht und allgemein kein wirklicher Ansatz da.

g'(x)= -8/x^2

Answer 1

hallo

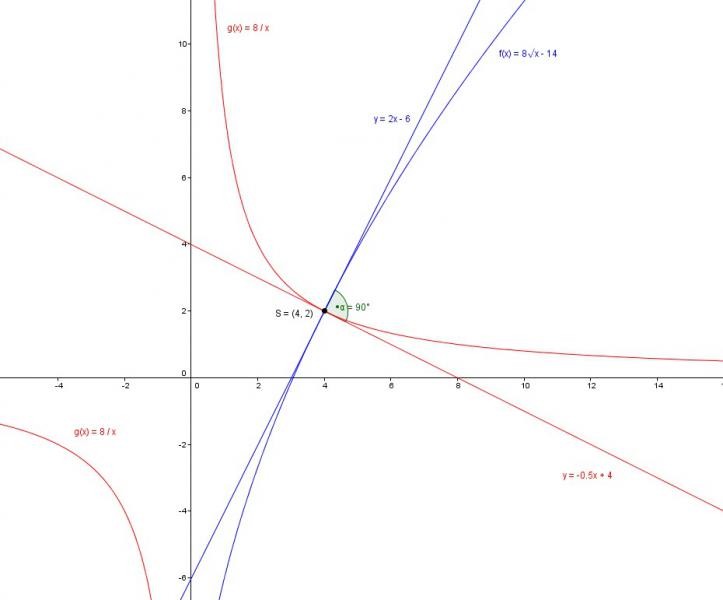
f(x)= 8√x -14
g(x)= 8/x

a)

f(4) = 8√2 - 14 = 2
g(4) = 8/4 = 2

f(4) =  g(4) = 2

(4|f(4)) = (4|2) ist gemeinsamer schnittpunkt von f und g.


b)

ich vermute man soll zeigen, dass f und g zueinander orthogonal sind.
das ist dann der fall, wenn die tangenten von f und g in einem punkt senkrecht aufeinander stehen.
das ist wiederum der fall, wenn f'(x₀) • g'(x₀) = -1 an der stelle x₀ gilt.

f'(x) = 4/√x
g'(x) = -8/x²

probieren wir mal den gemeinsamen schnittpunkt aus, ob dort die beiden tangenten senkrecht zueinander verlaufen.
f'(4) = 4/√4 = 2
g'(4) = -8/16 = -1/2
f'(4) • g'(4) = 2(-1/2) = -1

f(x) und g(x) sind also an der stelle x = 4 zueinander orthogonal.