Berechnen Sie, wie weit die Punkte A und C voneinander entfernt sind

Question

Aufgabe:

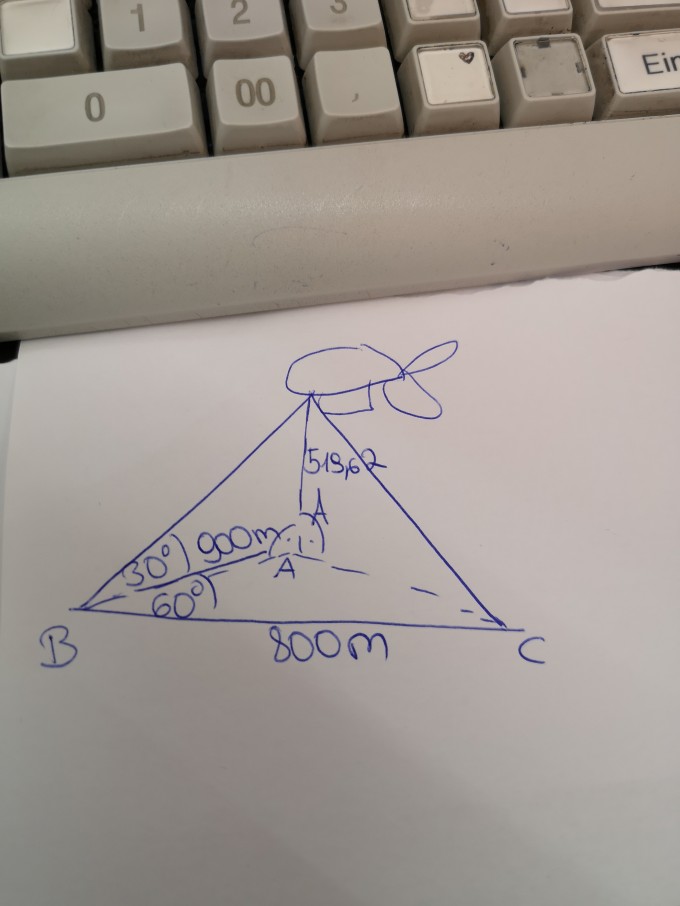
Ein Hubschrauber schwebt senkrecht über dem Punkt A. Eine Person beobachtet vom Punkt B aus den Hubschrauber unter einem Höhenwinkel von 30°.

Die Punkte A und B  liegen mit dem Hubschrauberlandeplatz C in derselben Horizontalebene. A und B sind 900 m voneinander entfernt. B und C sind 800m voneinander entfernt. Der Winkel ABC beträgt 60°. Berechnen sie wie weit die Punkte A und C voneinander entfernt sind.

Problem/Ansatz:

Ich komme da leider nicht weiter. Bitte um Hilfe

Comments

Der Hubschrauber spielt hier keine Rolle.

Answer 1

Hallo Maria,

sei x = Länge der Strecke AC in Metern.

dann gilt nach dem Kosinussatz

x² = 900² + 800² - 2·800·900·cos(60°)  (#)

\(x=\sqrt{900^2 + 800^2 - 2·800·900·cos(60°)}≈854,4\)

(#) Nachtrag:

https://de.wikipedia.org/wiki/Kosinussatz

Gruß Wolfgang

Comments

dankeee :) für deine anwort

---

aber wieso wurzel aus? die formel vond em kossinusssatz ist doch ohne wurzel aus

---

In der Zeile über der Wurzel steht ja ein x^2. Wir wollen aber die gesuchte dreiecksseite nicht als Quadrat ausrechnen sondern ganz normal, also x. Um das Quadrat weg zu bekommen, wird die Wurzel aus dem ganzen Ausdruck gezogen.

---

danke für deine antwort, war sehr hilfreich.

Answer 2

|AC| = \(\sqrt{800^2+900^2-2\cdot 800 \cdot 900 \cdot \cos 60°} \approx 854.4[m]\)

Comments

danke :) ich verstehe aber das wurzel aus überhaupt nicht