Wie weit waren zu diesem Zeitpunkt die Schiffe voneinander entfernt?

Question

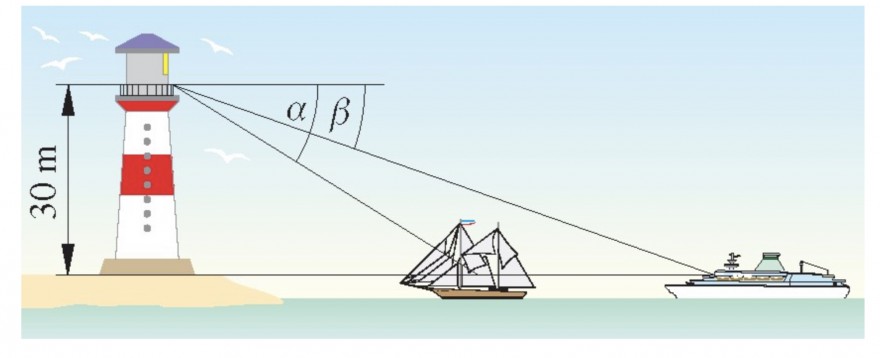
Aufgabe:

Zwei Schiffe werden auf gerader Linie von einem Leuchtturm aus angepeilt. Zur Entfernungsbestimmung der Schiffe wurden entsprechend der Skizze die Tiefenwinkel α = 15,7° und β = 12° gemessen. Wie weit waren zu diesem Zeitpunkt die Schiffe voneinander entfernt?

Answer 1

\(\begin{aligned}\frac{d_\text{Segler}}{30} &= \tan(90°-\alpha)\\\frac{d_\text{Yacht}}{30} &= \tan(90°-\beta)\\d&=d_\text{Yacht}-d_\text{Segler}\end{aligned}\)

Löse die Gleichungen.

Comments

Okayy und bekomme ich nochmal die gesamte Rechnung?

---

Setze erst ein mal die bekannten Werte ein und rechne soweit es geht aus.

---

Was bedeutet das D vor Segler und Yacht?

---

Ich habe den Abstand zwischen Leuchtturm und Segelboot \(d_\text{Segler}\) genannt.

---

Aber allgemein, weiß man ja nur Alpha und Beta?

---

Dann weiß man ja auch \(90° - \alpha\) und kann mit dem Taschenrechner \(\tan(90° - \alpha)\) berechnen. In der ersten Gleichung bleibt dann nur noch eine Variable übrig.

---

Ist das dann ungefähr 74,3

---

Was meinst du mit "das"?

• \(90°- \alpha\)
• \(\tan(90°- \alpha)\)
• \(d_\text{Segler}\)

---

Also das Ergebnis

---

Wovon soll 74,3 das Ergebnis sein?

---

Von der Aufgabe

---

74,3 ist nicht der Abstand der Schiffe voneinander.

---

Okay kann ich dann nochmal die ganze Rechnung bekommen damit ich weiß was ich noch nicht ganz richtig gemacht habeß?

---

Zeig mal deine Rechnung, dann kann ich dir erklären was du noch nicht ganz richtig gemacht hast.

---

Geht gerade leider nicht ):

---

Oder kommt raus 34,41 m?

Answer 2

30/TAN(12°) - 30/TAN(15.7°) = 34.41 m

Das könntest du aber auch anhand einer Skizze schnell prüfen

Comments

Hier noch etwas genauer