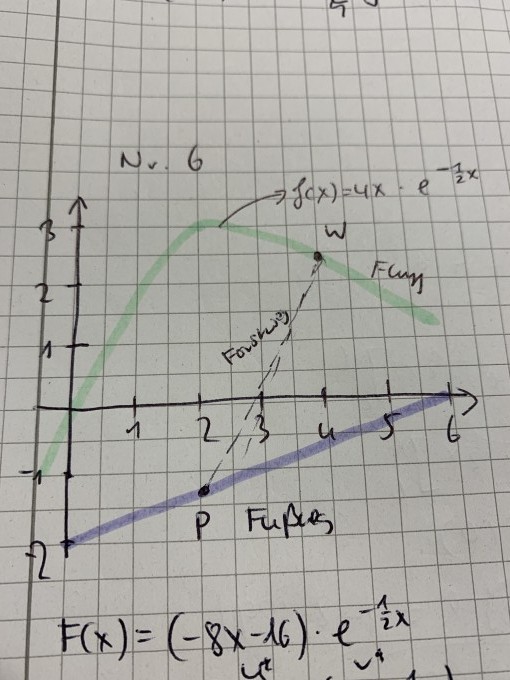
Aufgabe: Ein Waldstück wird nach Norden durch einen Fluss begrenzt, dessen Verlauf die Funktion f(x)= 4x* e^(-1/2x) beschreibt. Im Westen bildet eine in Nord-Süd-Richtung verlaufende Autobahn die Grenze, im Süden und Osten die abgebildeten Fußwege (1 LE= 1 km).
a) Bestimmen Sie die Lage des nördlichsten Punktes des Waldes.
c) Berechnen Sie die Waldfläche.
d) Unter welchem Winkel überbrückt die Autobahn den Fluss?
e) Im Wendepunkt des Flusses befindet sich eine Anlegestelle. Von dort verläuft senkrecht zum Fluss ein Forstweg. Wo trifft dieser auf den Fußweg?
Problem/Ansatz:
ich habe gerade die Aufgabe gelöst und würde mich freuen, wenn jemand mal darüber schauen würde und korrigieren kann, wenn erforderlich.
a) ich habe von f(x) die erste Ableitung gebildet, und zwar : f‘(x)= e^(-1/2x) (-2x+4). Dann f‘(x)=0, das ergibt dann 2. Der Hochpunkt liegt bei P(HP)= (2/2,943).
c) ich habe die Funktion P rekonstruiert: p(x)= 1/3x-2 . Dann im Intervall [0;6] integriert. Ich bekam die Fläche |-6|. Danach habe ich die Funktion f(x) im Intervall [0;6] integriert und bekam |-2,389|. Die Gesamtfläche beträgt 8,389.
d) ich habe so die Steigung berechnet f‘(0)=4 und bekam 4. danach tan^-1 (4)= 75,96 Grad.
e) da bin ich mir nicht so sicher. Ich habe die zweite Ableitung von f gebildet: f‘‘(x)= e^(-1/2x) (-4+x). Dann mit 0 gleichgesetzt. Es kam 4 raus. Dann in die Formel : d= Wurzel von (2-4)^2 + (4/3-2,1654)^2. dann kommt da 4,0300 raus.
Vielen Dank