Ich habe folgendes Problem: Und zwar komme ich bei dieser Aufgabe nicht weiter ://
In einer Fabrik werden Kugelschreiber hergestellt, anschließend ungeprüft in Packungen zu je 20 Stück verpackt und an Händler ausgeliefert. Weil sich viele Händler über die häufig unverkäuflichen Kugelschreiber beschweren, wird eine Endkontrolle eingeführt. Dabei wird ein Kugelschreiber mit einer WS von 10% als Ausschuss ausgesondert. Bei dieser Kontrolle wird erfahrungsgemäß ein einwandfreier Kugelschreiber mit einer WS von 4% als Ausschuss deklariert. Insgesamt sind 8,8% aller produzierten Kugelschreiber unverkäuflich.
a) Stellen Sie die Zusammenhänge mithilfe eines Baumdiagramms dar.
b) Berechnen Sie die WS dafür, dass ein unverkäuflicher Kugelschreiber aussortiert wird.
c) Berechnen Sie die WS dafür, dass ein Kugelschreiber wirklich unverkäuflich ist, falls er bei der Endkontrolle aussortiert wurde.
----------
Ich denke, ich kann b) und c) alleine berechnen, nur komme ich nicht darauf, wie das Baumdiagramm zu a) sein soll bzw. ich bin mir unsicher :/
Mein Ansatz:
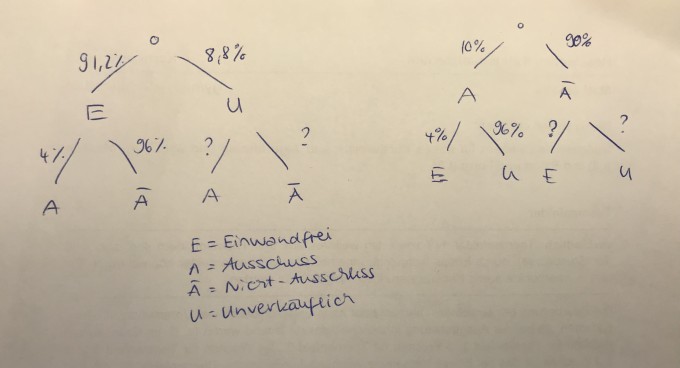
Ich wäre echt dankbar, wenn mir jemand helfen könnte, das Baumdiagramm richtig zu vervollständigen :)
!