Schnittpunkte von Geraden und Ebenen im skizzierten Quader

Question

gegeben sind die Ebene e: (1|-2|2) · vektor von x = 4,5 und die gerade g: vektor von x = (1|3|7) + λ · (-1|2|-2)

A) begründen sie, dass die gerade g die ebene e schneidet. Berechnen sie den Schnittpunkt.

B) entscheiden sie, ob die gerade g die ebene e senkrecht schneidet.

Bei der a muss ich ja lediglich den schnittpunkt berechnen, aber woran erkenn ich die b ?

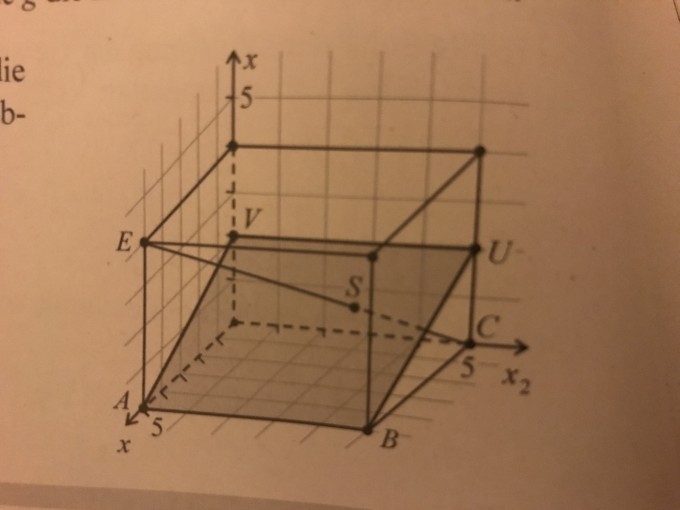
Zweite aufgabe:

In welchem punkt S schneidet die raumdiagonale EC die in der abbildung hervorgehobene fläche

Answer 1

Aloha :)

$$E:\;\left(\begin{array}{c}1\\-2\\2\end{array}\right)\vec x-4,5=0\quad;\quad g:\;\vec x=\left(\begin{array}{c}1\\3\\7\end{array}\right)+\lambda\left(\begin{array}{c}-1\\2\\-2\end{array}\right)$$Wenn ein Punkt \(\vec x\) der Geraden in der Ebene liegt, dann muss er die Ebenengleichung erfüllen. Also setzen wir die Geradengleichung einfach mal in die Ebenengleichung ein:$$\left(\begin{array}{c}1\\-2\\2\end{array}\right)\left[\left(\begin{array}{c}1\\3\\7\end{array}\right)+\lambda\left(\begin{array}{c}-1\\2\\-2\end{array}\right)\right]-4,5=0$$Die Skalarprodukte kann man im Kopf ausrechnen und findet:$$9-9\lambda-4,5=0\;\;\Leftrightarrow\;\;\frac{9}{2}=9\lambda\;\;\Leftrightarrow\;\;\lambda=\frac{1}{2}$$Dieses \(\lambda\) setzen wir in die Geradengleichung ein und finden als gemeinsamen Schnittpunt:$$\vec s=\left(\begin{array}{c}1\\3\\7\end{array}\right)+\frac{1}{2}\left(\begin{array}{c}-1\\2\\-2\end{array}\right)=\left(\begin{array}{c}\frac{1}{2}\\4\\6\end{array}\right)\quad\Leftrightarrow\quad \underline{S\left(\frac{1}{2};4;6\right)}$$

Bei (b) kannst du wie folgt argumentieren. Der Normalenvektor der Ebene ist \(\left(\begin{array}{c}1\\-2\\2\end{array}\right)\) und er steht senkrecht auf der Ebene. Der Richtungsvektor der Geraden ist exakt entgegengesetzt zum Normalenvektor der Ebene gerichtet (die Koordinaten sind negativ im Vergleich zum Normalenvektor). Daher schneidet die Gerade die Ebene senkrecht.

Answer 2

A) 1*(1-λ) - 2*(3+2λ) + 2*(7-2λ) = 4.5 ⇒ λ = 0.5   ⇒ S(0.5|4|6)

B) Das SP des NV der Ebene und des RV der Geraden ist genau dann null, wenn die Gerade normal zu der Ebene verläuft.

Comments

Du verwechselst S und V.

---

Das sp ist -9, also verläuft sie nicht senkrecht ?

---

Die Ebene ist doch in Hessischer NF dargestellt, oder nicht?