Aufgabe:
Der Würfel hat die Eckpunkte A(0| 0 |0) B(0 |8| 0) C(-8|8|0) E(0|0|8)
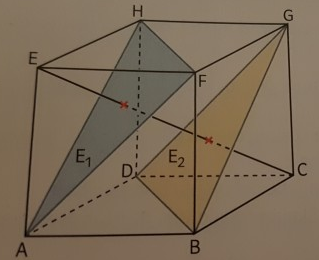
Die Ebene E1 ist durch die Punkte A, F und H, die Ebene E2 durch die Punkte B, D und G festgelegt.
a) Bestimmen Sie die Schnittpunkte der Geraden durch C und E mit den Ebenen E1 und E2
b) Peter behauptet, dass die Strecken EC durch die Schnittpunkte in frei gleichlange Stücke geteilt wird. Überprüfen Sie Peters Behauptung
Problem/Ansatz:
Könntet ihr den Rechenweg im Detail aufschreiben und wie ich überhaupt auf die Ebenengleichungen komme?
Lösungen a:
$$ E _ { 1 } : \vec { x } = r \cdot \left( \begin{array} { l } { 0 } \\ { 8 } \\ { 8 } \end{array} \right) + s \cdot \left( \begin{array} { r } { - 8 } \\ { 0 } \\ { 8 } \end{array} \right) \\ E _ { 2 } : \vec { x } = \left( \begin{array} { l } { 0 } \\ { 8 } \\ { 0 } \end{array} \right) + r \cdot \left( \begin{array} { r } { - 8 } \\ { - 8 } \\ { 0 } \end{array} \right) + s \cdot \left( \begin{array} { r } { - 8 } \\ { 0 } \\ { 8 } \end{array} \right) $$
$$g : \vec { x } = \left( \begin{array} { l } { 0 } \\ { 0 } \\ { 8 } \end{array} \right) + t \cdot \left( \begin{array} { r } { - 8 } \\ { 8 } \\ { - 8 } \end{array} \right)$$
Schnittpunkt von g mit E_{1}:
$$\mathrm { S } _ { 1 } \left( - \frac { 8 } { 3 } \left| \frac { 8 } { 3 } \right| \frac { 16 } { 3 } \right)$$
Schnittpunkt von g mit E_{2}:
$$\mathrm { S } _ { 2 } \left( - \frac { 16 } { 3 } \left| \frac { 16 } { 3 } \right| \frac { 8 } { 3 } \right)$$
Lösungen b:
Peter hat recht. Es ist:
$$\overline { E S _ { 1 } } = \sqrt { \left( 0 + \frac { 8 } { 3 } \right) ^ { 2 } + \left( 0 - \frac { 8 } { 3 } \right) ^ { 2 } + \left( 8 - \frac { 16 } { 3 } \right) ^ { 2 } } = \frac { 8 } { 3 } \sqrt { 3 }$$
entsprechend: \( \overline { \mathrm { S } _ { 1 } \mathrm { S } _ { 2 } } = \frac { 8 } { 3 } \sqrt { 3 } ; \overline { \mathrm { S } _ { 2 } \mathrm { C } } = \frac { 8 } { 3 } \sqrt { 3 } \)
Damit ist: \( \overline { E S _ { 1 } } = \overline { S _ { 1 } S _ { 2 } } = \overline { S _ { 2 } C } = \frac { 1 } { 3 } E C \)