Monotonie der Folge (√n)^(1/n) beweisen

Question

Aufgabe:

Monotonie bei Zahlenfolge (√n)^(1/n)


Gegeben sei die Zahlenfolge (√n)^(1/n) für n ∈ N.

Zeigen Sie, dass es ein n0 gibt, so dass die Folge für n ≥ n0 streng monoton fallend ist,
d.h. an > an+1 für alle  n ≥ n0 gilt.

Problem/Ansatz:

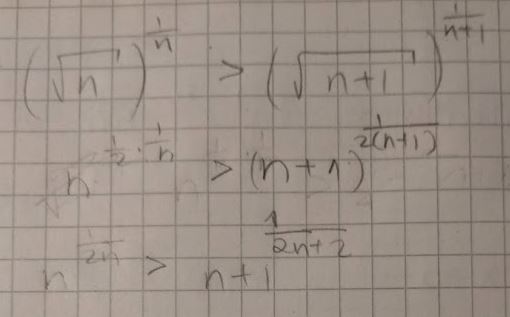
Ich kann von hier nicht weiter..

Ich dachte, ich sollte hier mit Logarithmus irgendwie die Potenzen weg kriegen, könnte bitte jemanden damit helfen?

Comments

Vom Duplikat:

Titel: Monotnoie bei Zahlenfolge (√n)^(1/n)

Stichworte: monotonie,folge

Gegeben sei die Zahlenfolge (√n)^(1/n) fur n ∈ N.

Zeigen Sie, dass es ein n0 gibt, so dass die Folge fur n ≥ n0 streng monoton fallend ist,
d.h. an > an+1 fur alle n ≥ n0 gilt.

---

Diese Frage wurde gestern bereits besprochen. Vgl. Antwort. Reagiere bitte dort.

@newbie: Es fällt auf, dass du erst einmal einen Stern für eine Antwort vergeben hast. Sind die andern Fragen noch offen? https://www.mathelounge.de/user/Mathe_newbie20/questions

Answer 1

Wenn du deine Ungleichung mit 2n*(2n+2) potenzierst (ist ja alles positiv)

bekommst du

n^(2n+2) > (n+1)^(2n)   | √...

<=> n^(n+1)  >  (n+1)^n

<=>  n* n^n  >  (n+1)^n    | : n^n

<=>  n >  ( (n+1)/n )^n

<=>  n >   (1 +1/n )^n

Die rechte Seite geht gegen e, ist also irgendwann sicherlich

kleiner als 3.

Comments

Wenn du die 2en weglässt, also mit n*(n+1) potenzierst, können die erste Zeile und die Wurzel wegfallen.