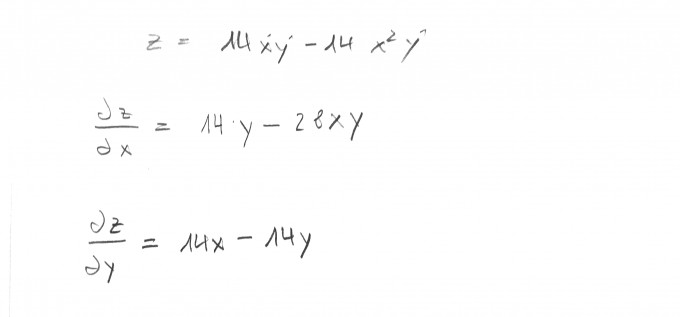Kettenregel Funktionen mit mehreren Variablen.

Question

Aufgabe:

Gegeben: $z = 14xy - 14x^2y.$
Bestimmen Sie $\frac{dz}{dt}$ mithilfe der Kettenregel. 
Drücken Sie ihre Antwort in $f$ aus. 
Ergänzung: Wobei $x = 6t$ und $y = 10(1-t)$
Tipp: $$\frac{dz}{dt}= \frac{\partial z }{\partial x}*\frac{dx}{dt}+\frac{\partial z }{\partial y}*\frac{dy}{dt}$$

Frage:

Ich konnte jeweils die Partielle Ableitung bilden.
Was mir fehlt ist noch dx/dt und dy/dt
Wie kriege ich diese?


Bild:

Comments

Wo kommt das t her ?
Sehe ich in der Funktion nicht.

---

Ergänzung: Wobei $x = 6t$ und $y = 10(1-t)$

---

Dann: dx/dt = 6 , dy/dt = -10

---

achsoo ? Warte, ich rechne das durch und dann poste ich es hier wieder ! :-)

---

Erste Seite:


---------------------------------------------------------------------------------------------------------------------------------------

Zweite Zweite Seite:

---------------------------------------------------------------------------------------------------------------------------------------

---

Du solltest doch dz/dt angeben (?)

Drücken Sie ihre Antwort in f aus.

Was ist denn f?

Answer 1

Mein Vorschlag
z = 14xy - 14x² * y
x = 6t
y = 10 * ( 1 - t )

z = 14xy - 14x² * y
z = 14 * ( xy - x² * y)
z ( t ) = 14 * ( 6 * t * 10 * ( 1 - t ) - 36*t² *( 10 * ( 1 - t ) ))
z ( t ) = 840 * t * ( 6*t² - 7*t + 1)
Differenzieren nach t