Funktionen mit mehreren Variablen. Ich habe eine Aufgabe bei der die Extremstellen zu bestimmen sind.
Folgende Funktion liegt vor:
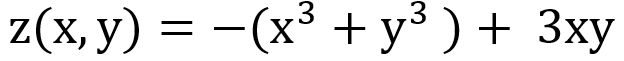
Text erkannt:
\( \mathrm{z}(\mathrm{x}, \mathrm{y})=-\left(\mathrm{x}^{3}+\mathrm{y}^{3}\right)+3 \mathrm{xy} \)
Die Partiellen Ableitungen sind folgende:
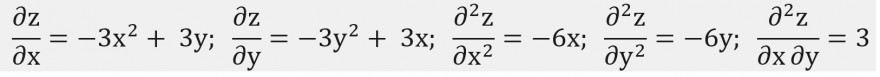
Text erkannt:
\( \frac{\partial \mathrm{z}}{\partial \mathrm{x}}=-3 \mathrm{x}^{2}+3 \mathrm{y} ; \frac{\partial \mathrm{z}}{\partial \mathrm{y}}=-3 \mathrm{y}^{2}+3 \mathrm{x} ; \frac{\partial^{2} \mathrm{z}}{\partial \mathrm{x}^{2}}=-6 \mathrm{x} ; \frac{\partial^{2} \mathrm{z}}{\partial \mathrm{y}^{2}}=-6 \mathrm{y} ; \frac{\partial^{2} \mathrm{z}}{\partial \mathrm{x} \partial \mathrm{y}}=3 \)
Problem:
Die ersten und zweiten partiellen Ableitungen habe ich verstanden, aber ich verstehe nicht die hier:
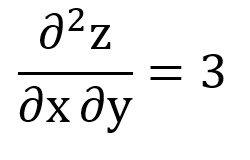
Text erkannt:
\( \frac{\partial^{2} \mathrm{z}}{\partial \mathrm{x} \partial \mathrm{y}}=3 \)
wurde hier nach beiden Variablen abgeleitet, wenn ja wie? Komme nicht auf das Ergebnis 3. Kann mir da jemand bitte den Rechenweg dazu zeigen? Ist glaube ich die zweite gemischte Ableitung
Danke.
LG