Geben Sie die Koordinaten eines Punktes B(xB /yB )an, so dass die Ableitung von f an der Stelle xB negativ ist.

Question

Aufgabe:

Geben Sie die Koordinaten eines Punktes B (xB /yB) an, so dass die Ableitung von f an der Stelle xB negativ ist.

Gegeben ist die Funktion f mit der Gleichung
f(x)= -x^3 + 2x^2
Problem/Ansatz:

Ich verstehe nicht was von mir gefragt ist bzw. was die Aufgabe bedeutet.

Answer 1

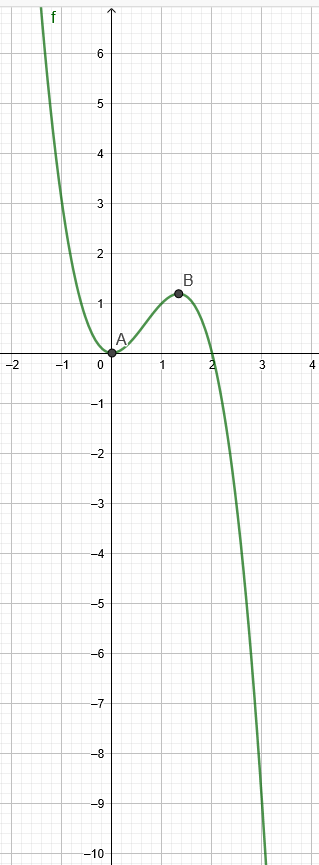
f(x)=-x^3+2x^2

f´(x)=-3x^2+4x

Extremwerte:

-3x^2+4x=0

x*(-3x+4)=0

x₁=0  →  f(0)=0

-3x+4=0

x₂=\( \frac{4}{3} \)     f(\( \frac{4}{3} \) )=-(\( \frac{4}{3} \) )^3+2*(\( \frac{4}{3} \) )^2=\( \frac{32}{27} \)

Art der Extremwerte:

f´´(x)=-6x+4

f´´(0)=4>0  Minimum

f´´(\( \frac{4}{3} \) )=-6*(\( \frac{4}{3} \) )+4<0 Maximum

Da nun das Minimum der Funktion in A(0|0) und das Maximum in B(\( \frac{4}{3} \)|\( \frac{32}{27} \)) liegen,sind zwischen dien Extremwerten die Steigung der Tangen in jedem Punkt positiv. Somit musst du außerhalb dieses Bereiches einen Punkt suchen.

Comments

Folgender Weg geht auch: f(x)=-x^3+2x^2

f´(x)=-3x^2+4x

Steigung soll nun negativ sein:

-3x^2+4x<0

x*(-3x+4)<0

1.)x<0

2.) -3x+4<0

-3x<-4|:(-3)

x>\( \frac{4}{3} \)