Kann mir bitte jemand erklären was ich hier tun soll?
Definition 1.28. Die Spannweite (Englisch: Range) einer Datenreihe x1,...,xn ist definiert durch
R:=x_{(n)}−x_{(1)}=
= max xi− min xi.
i=1,...,n i=1,...,n
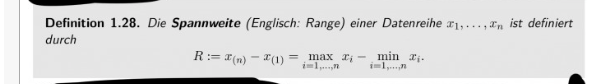
Weisen Sie nach, dass die im Skript in Def. 1.28 definierte Spannweite eines Datensatzes x1,...,xn die charakteristische Eigenschaft eines Skalenmaßes besitzt!
Gehen Sie folgendermaßen vor:
1. Betrachten Sie den veränderten Datensatz x′1, . . . , x′n mit x′i = axi + b für
i = 1, . . . , n und a, b ∈ R.
2. Notieren Sie die Spannweite wie eine Funktion, also R(x1, . . . , xn) bzw. R(x′1,...,x′n). Was muss für den Zusammenhang zwischen R(x′1,...,x′n) und R(x1, . . . , xn) gelten?
3 Stellen Sie eine Behauptung auf und beweisen Sie sie. Verwenden Sie im Beweis eine geeignete Fallunterscheidung.
Hier ist das Bild:
