Die sogenannte „Eckengleichheit“ platonischer und archimedischer Körper bedeutet insbesondere, dass in jeder Ecke gleichviele Kanten unter den gleichen Winkeln zusammentreffen. Alexander Heinz (Faltpolyeder, Bern 2019, ISBN 978-3-258-60198-4, Haupt-Verlag) ist auf die ausgezeichnete Idee gekommen, Eckelemente aus Papier zu falten, die ineinandergeschoben werden können und auf diese Weise zu Kantenmodellen von Körpern zusammengesteckt werden können. Dabei werden Eckelemente, in denen 3 Kanten zusammentreffen, aus je zwei gleichseitigen Dreiecken gefaltet. Entsprechend werden Eckelemente, in denen 4 Kanten zusammentreffen, aus je zwei Quadraten gefaltet. Regelmäßige Fünf- und Sechsecke sind dann die Grundelemente für Ecken, in denen 5 oder 6 Kanten zusammentreffen.
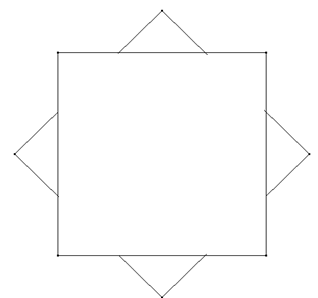
Das Falten eines Eckelementes mit 4 Kanten des späteren Körpers wird hier vorgeführt: Zwei Quadrate aus Papier werden in dieser Weise aufeinandergelegt (oben).
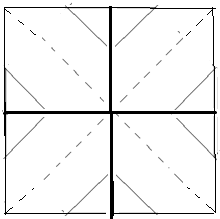
Die Ecken des unteren Quadrats werden über das obere Quadrat gefaltet. Weitere Faltungen erzeugen Bergfalten (fett) und Talfalten (gestrichelt). Diese Vorform des Moduls wird gewendet (oben).
Nach Faltung der Berg- und Talfalten entsteht ein Stern mit Einstecktaschen (als Folge des Wendens sind Berg und Tal vertauscht):
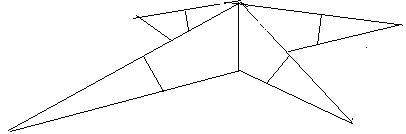
Die Abbildung zeigt eine Ecke des Kantenmodells eines Polyeders. Wie man leicht erkennt, kann ein durch das Modul ein bestimmter Winkel an der Polyederecke nicht unterschritten werden. Da aber die Winkel an Polyederecken festliegen, muss die Variationsbreite der Winkel des Moduls erhöht werden. Dies geschieht zum Beispiel, wenn man die Talfalten in Bergfalten umwandelt und zwischen je zwei Bergfalten eine Talfalte legt.
Beispiel: Falten einer Polyederecke mit Variationsbreite.
Zwei gleichseitige Dreiecke werden paarweise so aufeinandergelegt:
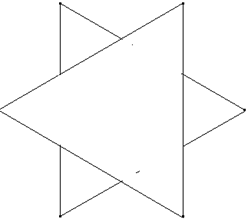
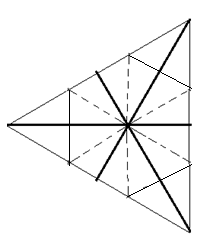
Die Ecken des unteren Dreiecks werden über das obere Dreieck gefaltet. Das Ganze wird gewendet und gefaltet. Bergfalten (fett) und Talfalten (gestrichelt). Die vom Mittelpunkt ausgehenden längeren Bergfalten sind Teile der Kanten des Kantenmodells und weisen Einstecktaschen auf.
Hat nun ein platonischer oder archimedischer Körper n Ecken, in denen jeweils m Kanten zusammentreffen. Dann benötigt man 2n regelmäßige m-Ecke, um die Moduln für das Zusammenstecken des Körpers zu falten.