Schnittpunkt mit der Y-Achse bestimmst du wenn du f(0) ausrechnest. D.h. 0 für x in die Funktionsgleichung einsetzen und Ausrechnen. Die Nullstellen bestimmt man indem man die Funktionsgleichung gleich 0 setzt. Bei Polynomen mit einem höheren Grad von 2 kann es nötig sein eine Nullstelle durch raten zu finden und dann eine Polynomdivision zu machen.
Bei den Folgenden Funktionen findest du alle Nullstellen über eine Wertetabelle im Bereich von -3 bis +3. Ich verzichte daher auf weitere Begründung und gebe die faktorisierte Form an, in der man auch die Nullstellen direkt ablesen kann.
a) f(x) = x^3 - 2·x^2 - 5·x + 6 = (x - 1)·(x + 2)·(x - 3)
b) f(x) = - x^3 + 5·x^2 - 8·x + 4 = (1 - x)·(x - 2)^2
c) f(x) = 0.5·x^3 + 1.5·x^2 - 2 = 1/2·(x - 1)·(x + 2)^2
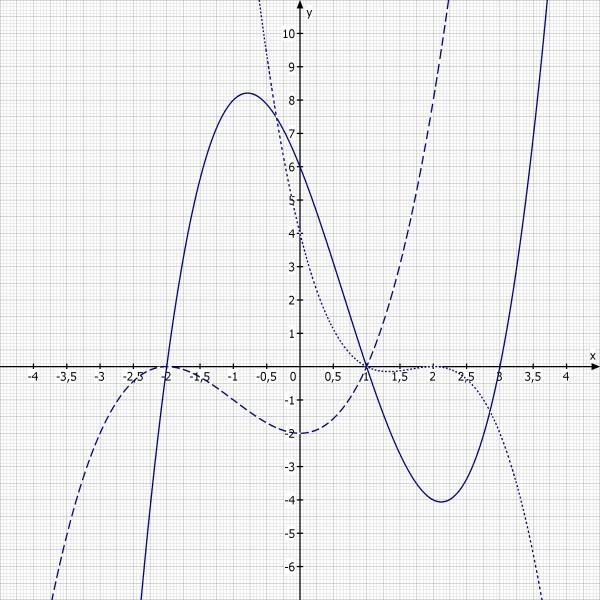
Hier noch eine Skizze aller Funktionen in einem Koordinatensystem