Stock AG Aufgabe Koeffizienten berechnen

Question

Aufgabe:

Sie werden von der Stock AG beauftragt, für das laufende Jahr eine Analyse des Lagerbestandes durchzuführen. Da das Lager bisher nur zweimal überprüft wurde, wissen Sie nur, dass zum Zeitpunkt t=95 der Lagerbestand 8863 Stück betrug und 124 Tage später 9646 Stück. Zu Beginn des Jahres (t=0) war das Lager leer. Aus Erfahrungen weiß man, dass der Lagerbestand nach folgender Funktion verläuft: L(t)=a⋅t hoch2+b⋅t+c

Markieren Sie die korrekten Aussagen.


a. Der Koeffizient des quadratischen Terms lautet 0.03.


b. Der Lagerbestand erreicht ein Maximum von 14696.59 Stück.


c. Die momentane Wachstumsrate an der Stelle t=272 beträgt −85.03 Stück.


d. Der durchschnittliche Lagerbestand im Intervall [154,275] beträgt 12150.56 Stück.


e. An der Stelle t=218 wird der Lagerbestand 11141.82 Stück betragen.

Problem/Ansatz:

kann mir hier jemand helfen? C ist ja 0 , ich weiß aber nicht genau wie man auf die Koeffizienten a und b kommt..

Comments

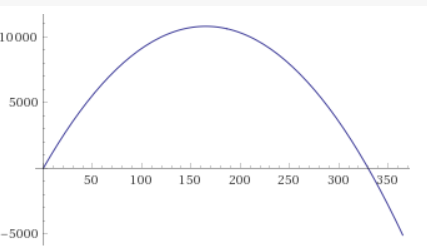
Du hast eine quadratische Gleichung L = at² + bt + c

Eine Parabel ist definiert wenn drei Punkte angegeben sind, und das ist bei dieser Aufgabe der Fall: (0 / 0), (95 / 8863), (95+124 / 9646).

Diese Werte kannst Du in die quadratische Gleichung einsetzen, und so erhält man ein Gleichungssystem mit drei linearen Gleichungen in drei Unbekannten:

0 = a0² + b0 + c

8863 = a95² + b95 + c

9646 = a219² + b219 + c

Wenn man das löst, erhält man die quadratische Gleichung als

L = -\( \frac{1024627}{2579820} \)t² + \( \frac{338023193}{2579820} \)t

 

Damit kommst Du hoffentlich weiter.

---

Zugabe:

Bei d) komme ich auf

Answer 1

Benutze: http://www.arndt-bruenner.de/mathe/scripts/steckbrief.htm

Eigenschaften

f(0)=0
f(95)=8863
f(219)=9646

Gleichungssystem

c = 0
9025a + 95b + c = 8863
47961a + 219b + c = 9646

Errechnete Funktion

f(x) = -1024627/2579820·x² + 338023193/2579820·x
f(x) = -0.3971699575·x^2 + 131.0258828·x

Fragen

a. Der Koeffizient des quadratischen Terms lautet 0.03.

falsch

b. Der Lagerbestand erreicht ein Maximum von 14696.59 Stück.

falsch

c. Die momentane Wachstumsrate an der Stelle t=272 beträgt −85.03 Stück.

richtig

d. Der durchschnittliche Lagerbestand im Intervall [154,275] beträgt 12150.56 Stück.

falsch

e. An der Stelle t=218 wird der Lagerbestand 11141.82 Stück betragen.

falsch