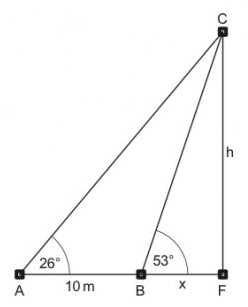
Die Höhe eines unzugänglichen Turmes soll mit Hilfe eines Höhenwinkelmessers bestimmt werden. Von zwei \( 10 \mathrm{m} \) voneinander entfernten Punkten A und B aus, die in einer Linie mit dem Fußpunkt F des Turmes liegen, werden die Höhenwinkel \( 26^{\circ} \) und \( 53^{\circ} \) gemessen.
a) Stelle im Dreieck BFC eine Beziehung zwischen \( \mathrm{h}, \mathrm{x} \) und dem Winkel \( 53^{\circ} \) auf und löse sie nach h auf. Stelle im Dreieck AFC eine Beziehung schen \( \mathrm{h}, \mathrm{x}+10 \) und dem Winkel \( 26^{\circ} \) auf und löse sie nach h auf.
b) Forme beide Gleichungen um zu einer Gleichung, die nur die Unbekannte \( x \) enthält und bestimme x.
c) Bestimme die Höhe h des Turmes.