Berechnung hervorgerufene Funktionsänderung mit Hilfe des totalen Differentials.

Question

Aufgabe:

Gegeben sei die Funktion

f(x1,x2)=e^{−0.15x1+0.2x2+0.45x1x2.}
Wie stark ändert sich die Funktion an der Stelle a=(2, 2.1), wenn das erste Argument um 0.9 steigt und das zweite Argument um 0.5 sinkt? Berechnen Sie die dadurch hervorgerufene Funktionsänderung mit Hilfe des totalen Differentials.

Problem/Ansatz:

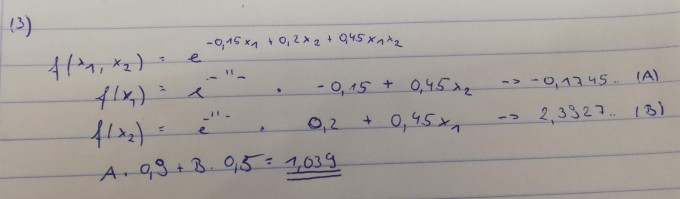
Text erkannt:

$3)$
$$\begin{aligned} f\left(x_{1}, x_{2}\right) &=e^{-0,15 x_{1}+0,2 x_{2}+945 x_{12}} \\ f\left(x_{1}\right) &=e^{-0,15 x_{1}+0,2 x_{2}+945 x_{12}} -0,15+0,45 x_{2} \quad -0,1745 \dot(A) \\ f\left(x_{2}\right) &=e^{-0,15 x_{1}+0,2 x_{2}+945 x_{12}} \cdot 0,2+0,45 x_{1} \quad 2,3927 \ \quad(B) \\ A \cdot 0,9+B \cdot 0,5 &=1,039 \end{aligned}$$

 Mein Ergebnis scheint nicht zu stimmen, kann mir jemand sagen wo ich falsch liege?

Answer 1

Du mußt Minus rechnen:

A*0.9 -B 0.5

erstmal die beiden Ableitungen:

f_x1=(0.45x₂ -0.15) e^(-0.15x₁ +0.2x₂+0.45x₁x₂)

fx₂=(0.45x_1 +0.2) e^(-0.15x₁ +0.2x₂+0.45x₁x₂)

Mein Ergebnis:

-0.698426

Comments

Bist du dir sicher, dass das Ergebnis stimmt? Selbst wenn ich minus rechne bekomme ich 1,2351..

---

ich rechne nochmal

---

hier das Ergebnis von Wolfram Alpha:

---

@grosserloewe: Wenn du bei Wolframalpha den ganzen Link (Browsereingabe) übernimmst und hier einfügst, kommt der User gratis zu deiner Eingabe in Wolframalpha und kann dann selbst allfällige Tippfehler in der Eingabe berichtigen.  (zumindest annähernd, der Editor hier macht manchmal doch etwas leicht anderes).

---

Ehm.. Ich muss für x1 und x2 doch 2 und 2.1 und nicht 0.9 und 0.5 einsetzen oder?

---

Ich muss für x₁ und x₂ doch 2 und 2.1 und nicht 0.9 und 0.5 einsetzen oder? --->JA

allg. gilt:

df= fx₁ *dx₁ +fx₂*dx₂

_{dx1= 0.9}

_{dx2= -0.5}

_{x1= 2.0}

_{x2= 2.1}

---

Aber wieso hast du dann in deiner Rechnung bei der e funktion 0.9 und und 0.5 eingesetzt? Tut mir Leid, dass ich so lästig nachfragen muss, aber bin gerade etwas verwirrt.

---

Dein Ergebnis stimmt.

---

Ah okay, danke!