Alle z Element von Komplexen Zahlen bestimmen für die gilt: (z+1)³ = i

Question

Aufgabe:

Bestimmen Sie alle z Element von den Komplexen Zahlen für die gilt: (z+1)³ = i

Problem/Ansatz:

Habe leider keine Ahnung wie ich die Aufgabe erledigen soll. Blindes umstellen auf z scheint mir eine Option zu sein aber wenn ich rumschaue stellen Leut die Polarkoordinaten auf - wäre sehr dankbar wenn jemand mir das vorgehen bzw. die Aufgabe vorrechnen könnte damit ich sehen kann, wie's erledigt wird!

Comments

Nach ein bisschen umstellen kriege ich:
z³+3z²+3z+1=i

Wie mir das hilft, weiß ich nicht.

Answer 1

Im ersten Schritt sucht man nach einer komplexen Zahl, deren dittte Potenz i ist. Da kommt am ehesten +i oder -i in Frage. Da von diesen möglichen Lösungen nur (-i)³=i gilt, ist mit -i die erste Lösung gefunden. Diese zeichnet man in die komplexe Zahlenebene ein. Da im Komplexen n-te Potenzen n Lösungen haben, deren Darstellungen sich in der komplexen Zahlenebene um den Winkel 360°/n voneinander unterscheiden, muss es drei Lösungen geben, die sich paarweise um 120° voneinander unterscheiden:

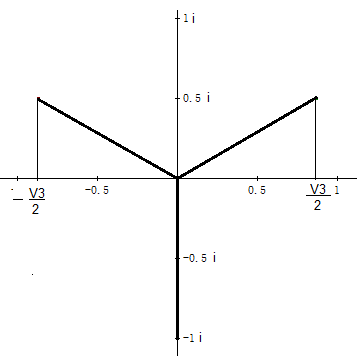
Also sind die anderen beiden Lösungen √3/2+i/2 und -√3/2+i/2.

Dann ist z-1 = -i           und z=1 - i
oder      z-1= √3/2+i/2 und z=1+√3/2+i/2
oder      z-1= -√3/2+i/2 und z=1 -√3/2+i/2. 

Comments

Danke Danke Das hilft mir massig weiter.