Aufgabe:
s.u.
Problem/Ansatz
Hallo. Stehe auf dem schlauch bei der Aufgabe unten. Ab dem Pfeil verstehe ich nicht wie man drauf kommt. Nach dem Schritt sind mir die Vereinfachungen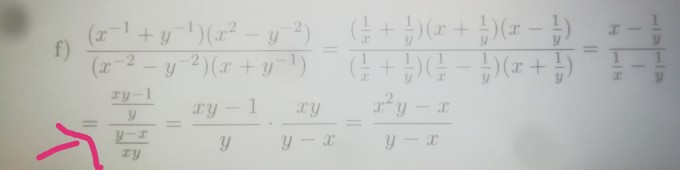
Text erkannt:
f) \( \frac{\left(x^{-1}+y^{-1}\right)\left(x^{2}-y^{-2}\right)}{\left(x^{-2}-y^{-2}\right)\left(x+y^{-1}\right)}=\frac{\left(\frac{1}{x}+\frac{1}{y}\right)\left(x+\frac{1}{y}\right)\left(x-\frac{1}{y}\right)}{\left(\frac{1}{x}+\frac{1}{y}\right)\left(\frac{1}{x}-\frac{1}{y}\right)\left(x+\frac{1}{y}\right)}=\frac{x-\frac{1}{y}}{\frac{1}{x}-\frac{1}{y}} \)
\( \Rightarrow=\frac{\frac{x y-1}{y}}{\frac{y-x}{x y}}=\frac{x y-1}{y} \cdot \frac{x y}{y-x}=\frac{x^{2} y-x}{y-x} \)
wieder klar.