Aufgabe:
Gegeben sei die Funktion $$ f(x)=x^{2}-2, \quad x \in \mathbb{R} $$
Es sei \( x_{0}=1 \) und die Funktionen \( t_{0}, t_{1}, t_{2}: \mathbb{R} \rightarrow \mathbb{R} \) sowie die Zahlen \( x_{1}, x_{2}, x_{3} \in \mathbb{R} \) seien rekursiv für \( j=0,1,2 \) folgendermaßen bestimmt:
i) Der Graph von \( t_{j} \) ist die Tangente an den Graphen von \( f \) an der Stelle \( x_{j} \)
ii) die Nullstelle von \( t_{j} \) ist \( x_{j+1} \)
a) Fillen Sie die folgenden Felder (außer den letzten beiden) der Tabelle aus.
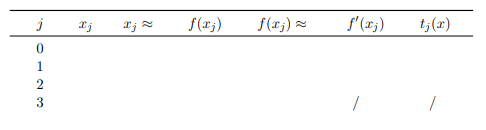
Problem/Ansatz:
Wie ist diese Tabelle auszufüllen? Tut mir leid, dass mit jeglicher Ansatz fehlt. Die Lösung würde mir helfen das ganze zu verstehen.