Berührpunkt einer Gerade mit einem Kreis

Question

an alle,

Gegeben ist der Kreis mit dem Radius 5mm und dem Mittelpunkt von (15/20). Außerdem gibt es noch einen Punkt P (10/5), durch den eine Gerade verläuft und den Kreis rechts berührt. Wie kann ich diesen Berührpunkt berechnen?

Danke

LG

Answer 1

Du könntest ein Paar von Funktionen aufstellen, also

$$f(x) = y_M + \sqrt{r^2 - (x-x_M)^2},~ g(x) = y_M - \sqrt{r^2 - (x-x_M)^2}$$

In deinem Fall mit $$y_M = 20, ~x_M = 15, ~r = 5$$.

Das würde so aussehen:

 

Jetzt kannst du die Geradengleichung mit diesen beiden Gleichungen gleichsetzen.

Wenn eine der beiden Gleichungen oder beide lösbar sind, hast du deinen Schnittpunkt bzw. Schnittpunkte mit dem Kreis.

Answer 2

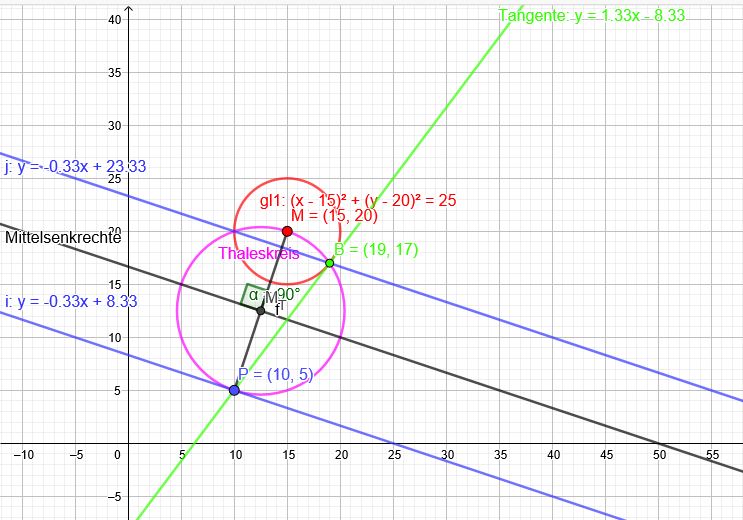
\(k:(x-15)^2+(y-20)^2=25\)      P \((10|5)\)

Der Thaleskreis über der Strecke \( MP\) schneidet den Kreis in den beiden Berührpunkten.

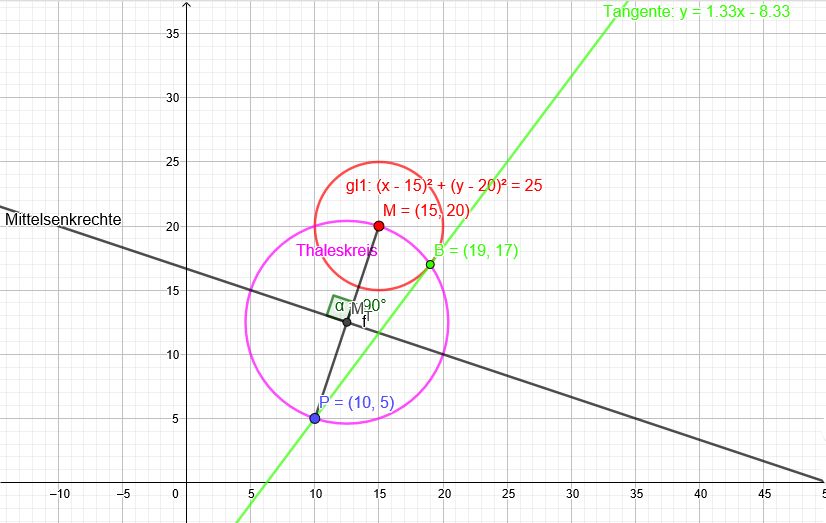
\(k(x,y)=(x-15)^2+(y-20)^2-25\)      P \((10|5)\)

\(k_x(x,y)=2(x-15)\)

\(k_y(x,y)=2(y-20)\)

\( k'(x)=-\frac{k_x(x,y)}{k_y(x,y)}=-\frac{x-15}{y-20}\)

\( k'(10)=-\frac{10-15}{5-20}=-\frac{1}{3}\)

Gerade durch P \((10|5)\) mit \(m=-\frac{1}{3}\)

\(\frac{y-5}{x-10}=-\frac{1}{3}\)

\(y=-\frac{1}{3}x+\frac{25}{3}\) liegt parallel zu der Passanten durch die beiden Berührpunkte.