Wie weit kann man bei klarer Sicht auf das Meer sehen, wenn man 80m hoch auf einem Leuchtturm steht?

Question

Liebe Community,

frage steht in der Überschrift, das Thema das wir gerade behandeln ist, wie in der Überschrift zu entnehmen die Satzgruppe des Pythagoras. Ich weiß aber nicht was ich mit (nur) einer Kathete anfangen soll, wenn ich nicht wenigstens einen Winkel habe bzw. eine andere Seitenlänge. :s

  :)

PS: Wir gehen davon aus, dass die Erde eine Scheibe ist.

Answer 1

PS: Wir gehen davon aus, dass die Erde eine Scheibe ist.

Dann kannst du bis zum Rand dieser Scheibe schauen, selbst dann, wenn du nicht auf dem Leuchtturm stehst.

 

Wenn man jedoch annimmt, dass die Erde eine Kugel ist (wenigstens in etwa), dann gibt es einen Horizont, also eine maximale Entfernung, bis zu der man die Erdoberfläche noch sehen kann. Weiter entfernte Objekte "verschwinden" dann "unter" dem Horizont.

Betrachte folgende Skizze:

 

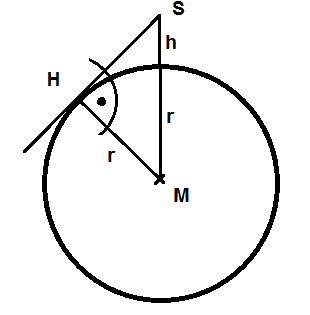
Das Dreieck MHS ist ein rechtwinkliges Dreieck. Seine Katheten sind die Strecken MH und SH, die Hypotenuse ist MS. Gesucht ist die Länge der Strecke SH

Die Länge der Strecke MH ist gleich dem Radius r der Kugel.

Die Länge der Strecke MS ist gleich dem Radius r zzgl. der Höhe h des Leuchtturms.

Daraus ergibt sich aus dem Satz des Pythagoras:

r ² + SH ² = ( r + h ) ²

<=> SH ² = ( r + h ) ² - r ² = r ² + 2 r h + h ² - r ² = h ² + 2 r h

<=> SH = √ ( h ² + 2 r h )

Setze für r den Radius der Erde und für h die Höhe des Leuchtturmes ein (auf gleiche Einheiten achten!) und rechne die Strecke SH aus. Das ist die gesuchte Blickweite.

Comments

Was soll man bei SH einsetzen?

---

Für SH sollst du nichts einsetzen, SH ist das gesuchte Ergebnis.