Guten Tag liebe Leute,
ich habe folgendes Schema gegeben:
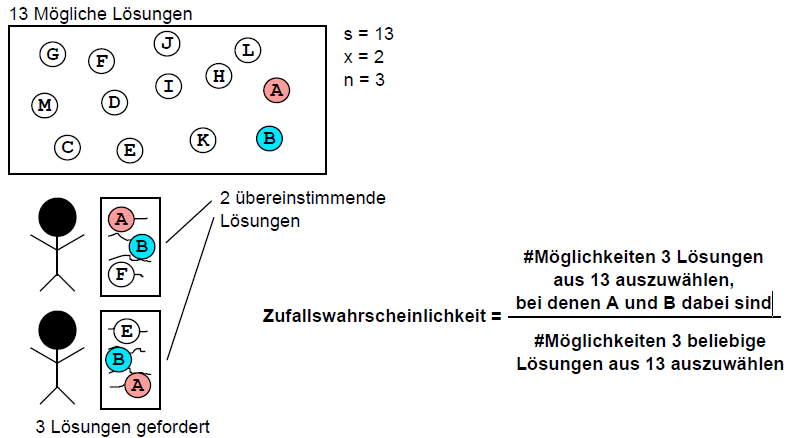
Ich möchte die Zufallswahrscheinlichkeit berechnen. Kurz zur Erklärung: Es giibt 13 mögliche Lösungen einer Aufgabe. Davon werden in diesem Fall 3 verschiedene Lösungen gefordert. Die Anzahl der übereinstimmenden Lösungen zweier Studenten ist in dem Fall 2. Ich möchte nun berechnen wie wahrscheinlich es ist, dass diese beiden nur zufällig die gleichen Lösungen abgegeben haben und nicht voneinander abgeschrieben haben. Das ganze soll allgemein erfolgen. Also die eben beschriebene Zufallswahrscheinlichkeit für beliebige s (>0), x (>0, <5) und n (>0, <5). Dazu ist wie man sieht angegeben, dass man die Zufallswahrscheinlichkeit errechnen kann, indem man die Anzahl der Möglichkeiten, 3 Lösungen (n) aus 13 (s) auszuwählen, bei denen A und B (x) dabei sind, durch die Anzahl der Möglichkeiten, 3 beliebige Lösungen (n) aus 13 (s) auszuwählen, teilt.
Im Nenner sollte meiner Ansicht nach der Binomialkoeffizient von 13 über 3, also s über n stehen. Aber ich bekomme einfach nicht raus, was ich in den Zähler schreiben muss. Ich sitze nun seit 3 Tagen daran und habe schon etliches ausprobiert, aber es kommt nie das richtige Ergebnis raus. Ich wäre euch sehr dankbar, wenn ihr mir helfen könntet. Vielen Dank schonmal im Voraus.
Marcel