Stochastik: Galton-Brett für n = 5. Die kleinen Dreiecke sind Hindernisse

Question

Hallo. Wie löse ich diese Aufgabe?

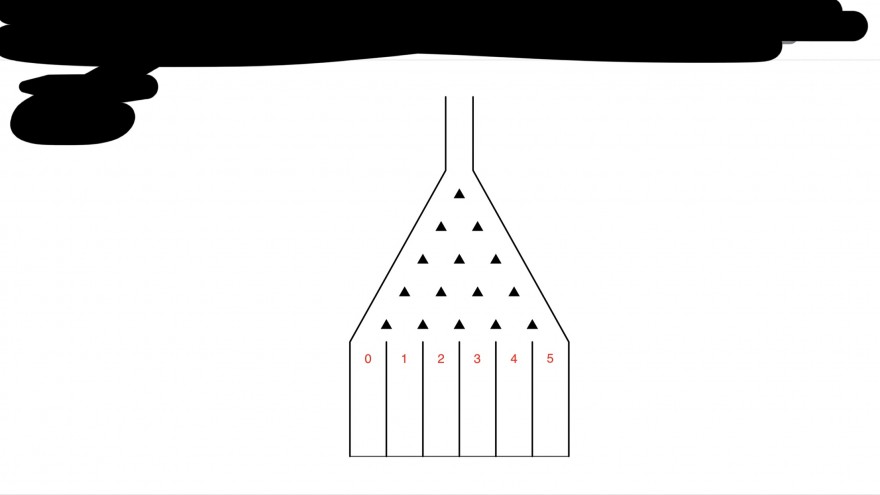
Die Graphik zeigt ein Galton-Brett für n = 5. Die kleinen Dreiecke sind Hindernisse, an denen eine Kugel, die man oben in die Öffnung fallen lässt entweder nach links oder rechts unten weiter rollen muss. Zuletzt landet die Kugel in einem der sechs Auffangbehälter.

(a) Wir betrachten die möglichen Wege, die eine Kugel zurücklegen kann:
i. Wie viele Wege gibt es, so dass die Kugel in Fach 0 landet?
ii. Wie viele Wege gibt es, so dass die Kugel in Fach 1 landet?
iii. Wie sieht es mit \( k \in\{2,3,4,5\} \) aus? Wie viele Wege gibt es für die einzelnen Fächer? Begründen Sie ihre Aussage jeweils kombinatorisch!
(b) Verallgemeinern Sie die Aussage für ein Galton-Brett mit \( n+1 \) Fächern für beliebiges \( n \in \mathbb{N} . \) Geben Sie die mögliche Anzahl der Wege für ein Fach \( k \) mit \( k \in\{0,1, \ldots, n\} \)
an.

Answer 1

a) i) Es gibt nur einen Weg (5 über 0)

a) ii) 5 Wege (5 über 1)

a) iii) (5 über k) = 5! / (k! * (5 - k)!)

b) (n über k) = n! / (k! * (n - k)!)

Comments

Wie kommen Sie bei b) auf die fünf Wege? Ich hatte versucht die Abbildung irgendwie in ein Baumdiagramm zu übersetzen aber das bringt nichts?

---

Welche Zusammenhänge gibt es zwischen dem Galton-Brett, dem Pascalschen Dreieck und der folgenden Aussage?

Welche Zusammenhänge gibt es zwischen dem Galton-Brett, dem Pascalschen Dreieck und der folgenden Aussage?
n+1 n n k+1=k+k+1
Beweisen Sie die in (c) genannte Aussage für n ∈ N und 0 ≤ k ≤ n.

---

Welche Zusammenhänge gibt es zwischen dem Galton-Brett, dem Pascalschen Dreieck und der folgenden Aussage?

Zeichne dir das Paskalsche Dreieck bis zu der Zeile auf in der Du 6 Zahlen nebeneinander stehen hast. Was fällt dir an den Zahlen auf? Sind das genau die Anzahl Pfade, die im Feld k von 0 bis 5 enden ?