ich habe Teilaufgabe a gelöst. Hier der Ansatz; die Verallgemeinerung ist dann kein Problem mehr.

Text erkannt:
\( \{(m, 1) \)
7. \( \quad \) zergess \( \quad \) Stab \( (k)<6 \)
7 ersen an Beirriel. Peweil
\( G<s_{y m_{1}} \)
\( S_{Y m_{1}}=\left(\left\{\left(\begin{array}{ccc}1 & 2 & 3 \\ 7 & 2 & 3\end{array}\right),\left(\begin{array}{ccc}1 & 2 & 3 \\ 1 & 3 & 2\end{array}\right)_{1}\left(\begin{array}{ccc}2 & 2 & 3 \\ 2 & 1 & 3\end{array}\right)_{1}\right.\right. \)
3.1
\( G-\left(\left\{\begin{array}{lll}1 & 2 & 3 \\ 1 & 2 & 3\end{array}\right),\left(\begin{array}{lll}1 & 2 & 3 \\ 1 & 3 & 2\end{array}\right),\left(\begin{array}{lll}1 & 2 & 3 \\ 2 & 1 & 3\end{array}\right)\right. \)
\( \left.\left.\left(\begin{array}{lll}1 & 2 & 1 \\ 3 & 2 & 1\end{array}\right)\right\}_{1} \cdot 0\right) \)
Probe 1,6 abjeralaries?
\( \sin 6(1)<G \)
\( 5+a b+(1)=\{9 \in 9 | 8(1)=13 \)
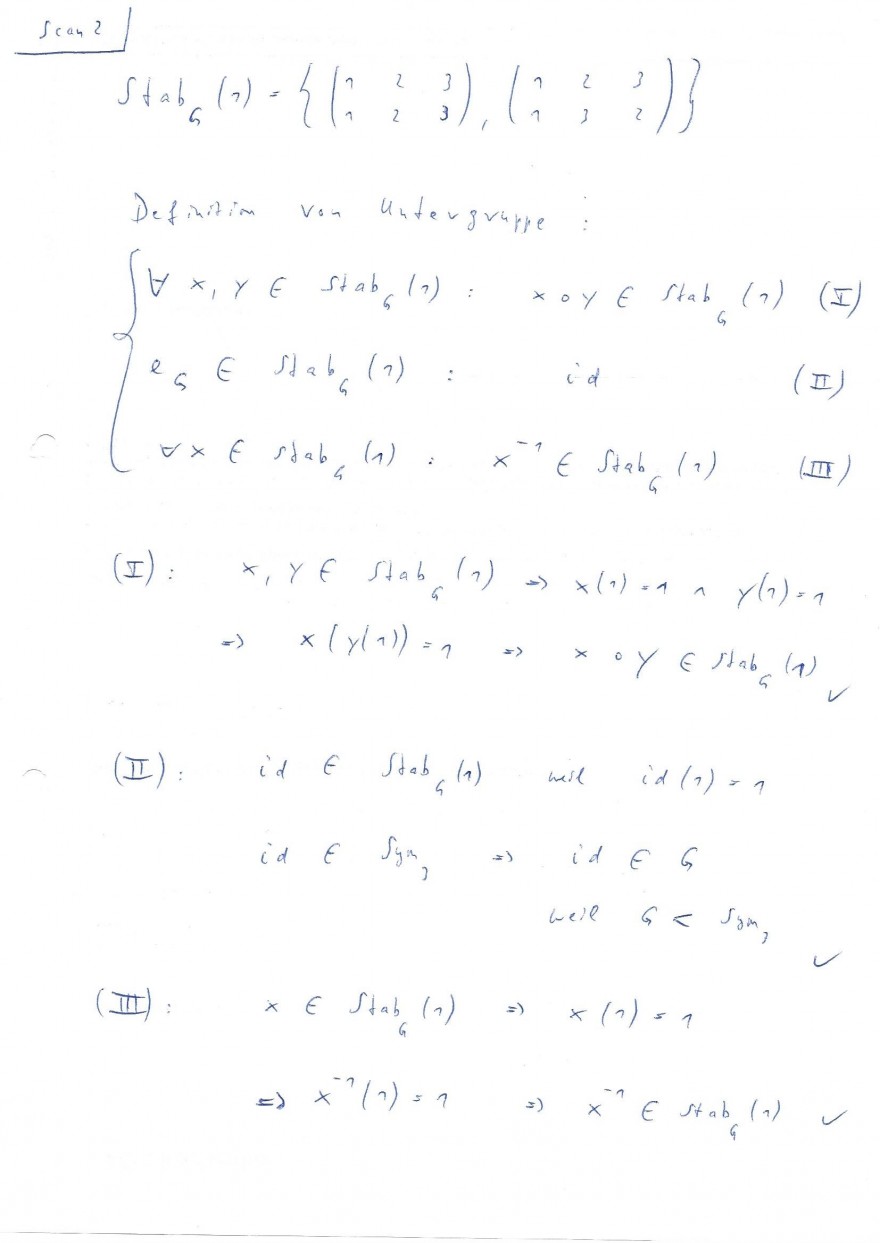
Text erkannt:
\( \frac{\sin 2}{\operatorname{stan}_{6}(x)}=\left\{\left(\begin{array}{ccc}1 & 2 & 3 \\ 1 & 2 & 3\end{array}\right),\left(\begin{array}{ccc}1 & 2 & 3 \\ 1 & 3 & 2\end{array}\right)\right\} \)
Definitim vou unterguarre \( \left\{\begin{array}{l}\forall x_{1}, \gamma \in \sin b_{6}(x)=x_{0} y \epsilon \sin b_{6}(x)(5) \\ e_{5} \in \sin b_{6}(x): \quad i_{0} \\ \sigma x \epsilon_{1} \sin b_{4}(1), \quad x^{-1} \in \sin 6_{6}(1) \quad(\pi)\end{array}\right. \)
\( (I): \quad *, y \in \sin 6(x) \rightarrow x(1) \cdot 1 \quad \cdot \quad y(1)=1 \)
\( \Rightarrow \quad x(y(1))=1 \quad \Rightarrow \quad x \cdot y \in \sin _{10}(y) \)
\( (\underline{I}): \quad \) id \( \quad \epsilon \quad \int d_{a b}(x) \quad \) mil
\( i d(1)=1 \)
id \( \epsilon \quad f_{y_{2}}, \quad \Rightarrow \quad \) id \( \quad \in \quad G \)
well \( G<J_{i m} \)
\( (\mathbb{I I}) \)
\( x \in S+a b_{G}(1) \Rightarrow x(1)=1 \)
\( \Rightarrow x^{-1}(\eta)=1 \quad \Rightarrow \quad x^{-1} \in \quad \sin ^{b}(1) \)