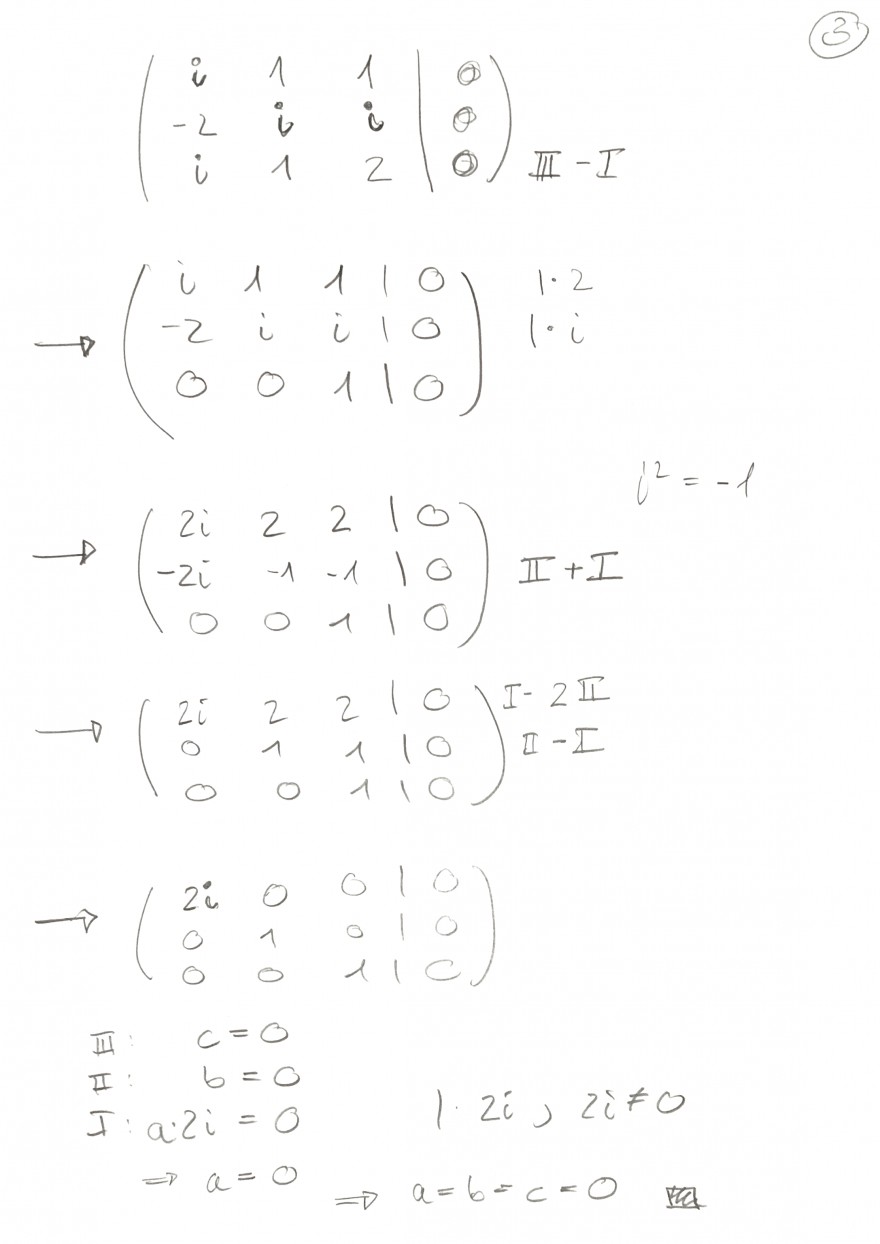Aufgabe Lineare Algebra - Hab ich Gauss mit komplexen Einträgen richtig durchgeführt?

Question

Aufgabe:

In einer Aufgabe will ich Basismatrizen auf lineare Unabhängigkeit prüfen.

Ausgehend vom Gleichungssystem 

1:     a*i +   b       + c    = 0 
2:   -2*a +   b*i    + c*i  = 0
3:     a*i +   b      + 2*c  = 0 

Bekomme ich per Hand gelöst folgendes über: (Zuunterst Bild) 

Problem/Ansatz:

Die Webseite Matrixcalc hat zwar die gleichen Lösungen, jedoch 
führt sie diese Rechnung anders aus. 
Weil ich mit komplexen Zahlen nicht so vertraut bin, weiss ich nicht ob ich irgendwo einen Fehler gemacht habe.

Bin für jede Hilfe dankbar ! 


Bild (Seite 1) :

Seite 2: Gaussalgorithmus Hier eventuel Fehler:
 

Comments

Matrixcalc-link mit Lösung: 

https://matrixcalc.org/de/slu.html#solve-using-Gaussian-elimination%28%7B%7Bi,1,1,0,0%7D,%7B-2,i,i,0,0%7D,%7Bi,1,2,0,0%7D%7D%29

---

Wie lautet der zugrunde liegende Körper?

R oder C ?

---

Der zugrundeliegende Körper ist C

Answer 1

Seite 1, Zeile 6: "z.z.:" statt "Es gilt".

Alles richtig!

Seite2: Das ist kein Gauss, aber alle Matrizenmanipulationen sind erlaubt. Bei Gauss wird die Pivotzeile abgeschrieben.

Rechnung und Ergebnis sind ohne Fehler: lin. unabh.

Answer 2

Warum machst du nicht "einfach" die Einsetzprobe? Passt das denn nicht?

Ausserdem: Dein Link hat dasselbe Resultat.

Das zweite Bild "Seite 2: Gaussalgorithmus" ist alles, was du brauchst.

Du bist fertig, wenn du die Dreiecksmatrix hast und in der Hauptdiagonalen keine 0 steht.

D.h. du brauchst nicht bis zur Diagonalform weiterzurechnen.

Comments

Vielen Dank ! 

Was meinst du mit Einsetzprobe ?

---

Vielleicht war das für dich klar, da a=b=c=0 immer stimmt. Dein Link findet aber auch keine anderen Lösungen.

Der Rechenweg muss nicht zwingend gleich aussehen. Es genügt, wenn die Lösungsmenge gleich ist.

"Gauss2 ist übrigens eine ganz bestimmte Art der Matrix-Manipulation, die sich aber nicht unbedingt für das schnelle Rechnen von Hand eignet. https://de.wikipedia.org/wiki/Gau%C3%9Fsches_Eliminationsverfahren#Pivotisierung

vs. https://de.wikipedia.org/wiki/Gau%C3%9F-Jordan-Algorithmus