Magische n×n-Quadrate für ungerade Zahlen n können nach einer einheitlichen Regel hergestellt werden, die für n=5 vorgeführt wird:
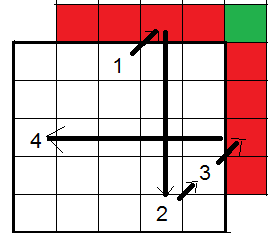
Ins mittlere Feld der obersten Zeile wird die 1 eingetragen und es folgen die Eintragungen der Zahlen 2, 3, 4 usw. fortlaufend in der Bewegungsrichtung schräg rechts nach oben. Kommt man auf diesem Wege auf ein rotes Feld, muss man auf die Gegenseite zurück. Kommt man auf ein besetztes oder auf ein grünes Feld, muss man die nächste Zahl im Feld direkt unter der letzten Eintragung weiter machen.
Zum ersten Mal tritt diese Situation ein, wenn nach der 5 die 6 eingetragen werden soll, die dann direkt unter der 5 eingetragen wird.
Magische n×n-Quadrate für Zahlen n=4k können ebenfalls nach einer einheitlichen Regel hergestellt werden, die für n=8 vorgeführt wird:
Zunächst wird das ganze Quadrat in 4×4-Felder aufgeteilt, deren Diagonalen jeweils markiert werden.
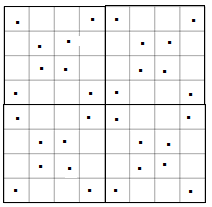
Dann werden die Felder fortlaufend Zeile für Zeile von oben nach unten und von links nach rechts durchnummeriert, wobei die markierten Felder ohne Eintragung bleiben.
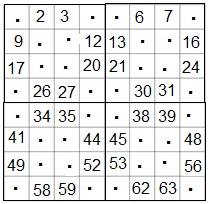
Nun werden die Felder fortlaufend Zeile für Zeile von rechts nach links und von unten nach oben durchnummeriert, wobei die besetzten Felder nicht neu beschriftet bleiben.
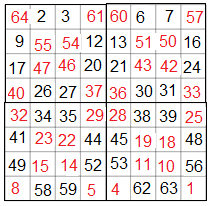
Damit sind aber bei weitem nicht alle bekannten Konstruktionsprinzipien magischer Quadrate genannt. Ein weiteres Konstruktionsprinzip stützt sich auf eine Lösung eines vereinfachten eulerschen Offiziersproblems:
Zu einer Militärparade in St. Petersburg haben 4 verschiedene Regimenter r, s, t, u je 4 Vertreter mit verschiedenen Dienstgraden w, x, y, z entsandt. Diese sollten bei der Parade in einem Quadrat aufmarschieren und zwar so, dass in jeder der 4 Zeilen und jeder der 4 Spalten sowohl jeder Dienstgrad als auch jedes Regiment vertreten ist.
Zur Lösung bilden wir die Quadrate aus den Regimentsbezeichnungen r, s, t, u bzw. den Dienstgradbezeichnungen w, x, y, z in der Weise, dass pro Quadrat in jeder Zeile und in jeder Spalte jeder Buchstabe genau einmal vorkommt:
\( R = \begin{pmatrix} r & s&t&u \\ s & u&r&t\\ u&s&t&r\\t&r&u&s \end{pmatrix} \) und \( D= \begin{pmatrix} z & y&w&x\\x&w&y&z\\y&z&x&w \\ w & x&z&y \end{pmatrix} \)
Nun bilden wir aus der Matrix R der Regimenter und aus der Matrix D der Dienstgrade eine weitere Matrix nach der Regel:
Aus aik є R und bik є D wird (aik,bik).
Damit ist das vereinfachte Offiziersproblem gelöst, doch was hat das mit magischen 4×4-Quadraten zu tun? Wir ordnen jedem der Buchstaben r, s, t, u aus R genau eine der Zahlen 1, 2, 3, 4 sowie jedem der Buchstaben w, x, y, z aus D genau eine der Zahlen 0, 4, 8, 12 zu. Dann ist R+D ein magisches Quadrat.
Beispiel: Sei r=2, s=4, t=3, u=1 sowie w=0, x=8, y=12, z=4. Dann gilt:
\( R=\begin{pmatrix} 2 & 3&4&1\\4&1&2&3\\1&4&3&2 \\ 3 & 2&1&4 \end{pmatrix} \) und \( D=\begin{pmatrix} 4 & 12&0&8\\8&0&12&4\\12&4&8&0 \\ 0 & 8&4&12 \end{pmatrix} \)
Und dann ist \( R+S= \begin{pmatrix} 6 &15&4&9\\12&1&14&7\\13&8&11&2 \\ 3 & 10&5&16 \end{pmatrix} \), also die Matrix eines magischen Quadrats.
Insgesamt lassen sich nach diesem Konstruktionsprinzip 4! · 4! = 576 verschiedene magische 4×4-Quadrate herstellen, wenn man Drehungen und Spiegelungen als unterschiedlich ansieht und dies sind nicht einmal alle, die möglich wären.