Folgt man den Anleitungen aus dem Artikel: 'Aufteilung magischer Quadrate in Teilquadrate | Mathelounge' , so lassen sich auch allgemeine Regeln für die Konstruktion magischer Quadrate ungerader Ordnung sowie durch 4 teilbarer Ordnung erkennen. Die direkte Anwendung dieser Regeln führt dann zu Konstruktionsmethoden für magische Quadrate der Ordnung 3, 4, 5, 7, 8, 9, 11, 12, 13, 15, 16, 17 und so weiter. In dieser Folge natürlicher Zahlen fehlen die doppelten Primzahlen. Im Folgenden wird eine Methode zur Konstruktion magischer Quadrate mit einfach-gerader Ordnung genannt. Ein Quadrat mit einfach gerader Ordnung hat eine Kästchenanzahl pro Seite, die durch 2 teilbar ist aber nicht durch 4. Dies schließt die hier zu konstruierenden Quadrate ein, deren Ordnung das Doppelte einer Primzahl ist. Eine etwas unglückliche Beschreibung dieser Konstruktionsmethode findet man bei ‚WikiHow‘.
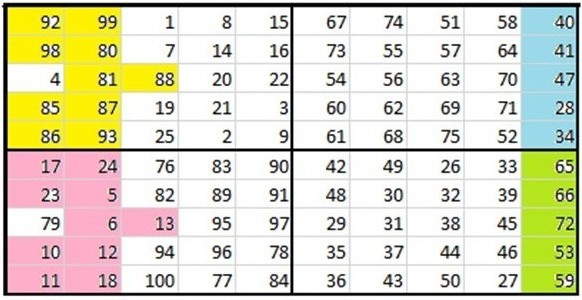
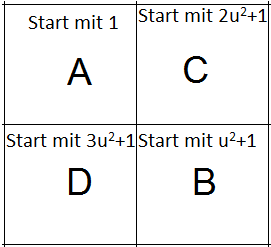
Sei u eine ungerade Zahl, dann hat ein Quadrat mit einfach gerader Ordnung die Kästchenzahl 2·u pro Seite und lässt sich in 4 Quadrate der Ordnung u aufteilen. Jedes dieser 4 Teilquadrate A, B, C und D (Anordnung siehe unten) wird nach dem Konstruktionsprinzip für Quadrate mit ungerader Ordnung ausgefüllt. Dabei beginnt das Ausfüllen von Quadrat A mit 1, das Ausfüllen von Quadrat B mit u2+1, das Ausfüllen von Quadrat C mit 2u2+1 und das Ausfüllen von Quadrat D mit 3u2+1:
Nach Fertigstellung dieses Arbeitsschrittes stellt man fest, dass alle Spaltensummen identisch sind, nicht aber die Zeilensummen. Im nächsten Arbeitsschritt müssen nun einige Zahlen ihre Zeile wechseln, ohne ihre Spalte zu ändern. Die davon betroffenen Zahlen im Quadranten A werden folgendermaßen markiert:
In der oberen linken Ecke des Quadranten A wird ein Quadrat von (u-1)/2×(u-1)/2 Kästchen markiert und ebenso in der unteren linken Ecke des Quadranten A. Dazwischen wird (um 1 Kästchen nach rechts gerückt) eine Zeile von (u-1)/2 Kästchen markiert:
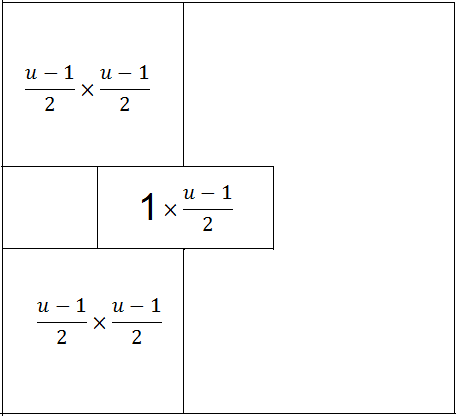
Diese Felder des Quadranten A werden 1:1 mit den kongruent entsprechenden Feldern des Quadranten D getauscht.
Im Quadranten C werden die letzten (u-3)/2 Spalten markiert und mit den kongruent entsprechenden Feldern des Quadranten B getauscht.

Exemplarisch für die Anwendung der Vertauschungsregeln des zweiten Konstruktionsschrittes werden diese auf die Konstruktionsregeln zunächst eines 6×6-Quadrates und dann eines 10×10-Quadrates angewendet:
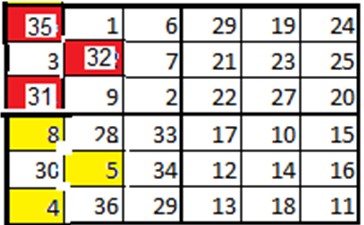
In einem 6×6-Quadrat ist u=3, (u-1)/2=1 und (u-3)/2=0. Ausgetauscht werden also die gelb markierten Felder gegen die rot markierten Felder:
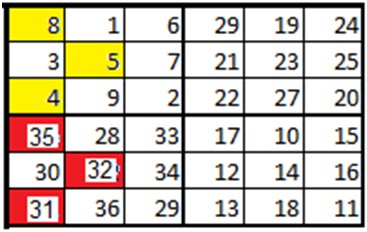
Und es entsteht:
In einem 10×10-Quadrat ist u=5, (u-1)/2=2 und (u-3)/2=1. Ausgetauscht werden also die gelb markierten Felder gegen die rot markierten Felder sowie die grün markierten Felder gegen die blau markierten Felder mit diesem Ergebnis: