\( \begin{pmatrix} 0&5&0 & 5&5&0 \\ 1&1&4 & 4&1&4 \\ 3&2&2 & 2&3&3\\ 2&3&3 & 3&2&2\\ 4&4&1 & 1&4&1\\ 5&0&5 & 0&0&5 \end{pmatrix} \)
Diese Matrix A hat folgende fünf Eigenschaften:
- Alle Zeilen- und alle Spaltensummen sind 15.
- In jeder Spalte kommt jede der Zahlen 0 bis 5 genau einmal vor.
- In jeder Zeile stehen genau zwei verschiedene Zahlen.
- Beide Diagonalen lauten von oben nach unten 0, 1, 2, 3, 4, 5.
- Keine Spalte kommt doppelt vor.
Spiegelt man A an der Diagonale, die von links unten nach rechts oben verläuft und addiert zu jeder der 36 Zahlen eine 1, so erhält man Matrix B
\( \begin{pmatrix} 6&2&3 & 4&5&1 \\ 1&5&3 & 4&2&6 \\ 1&2&4 & 3&5&6\\ 6&2&4 & 3&5&1\\ 1&5&4 & 3&2&6\\ 6&5&3 & 4&2&1 \end{pmatrix} \)
Aus A und B lässt sich mit 6A+B das folgende magische 6×6-Quadrat konstruieren:
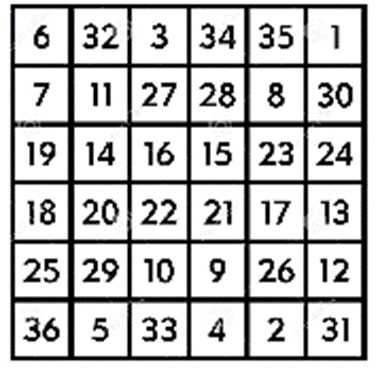
Wenn man als Ausgangsmatrix A irgendeine wählt, welche die fünf oben genannten Eigenschaften hat, gelingt die Konstruktion eines magischen 6×6-Quadrates.