Ein magisches 12×12-Quadrat lässt sich aus 16 3×3-Quadraten zusammensetzen, die alle die magische Eigenschaft der gleichen Zeilen-, Spalten- und Diagonalensumme haben, aber diese Summe ist in jedem 3×3-Quadrat anders. Um ein solches magisches 12×12-Quadrat zu konstruieren, benötigen wir im ersten Schritt ein magisches 3×3-Quadrat und ein magisches 4×4-Quadrat. Ein magisches 3×3-Quadrat konstruiert man z.B. so:
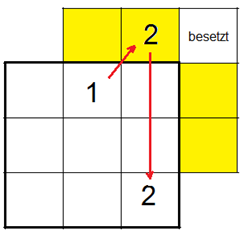
Man beginnt oben in der Mitte mit 1 und bewegt sich in nordöstlicher Richtung weiter, um die nächsten Zahlen einzutragen. Gerät man auf diesem Wege auf ein gelbes Feld, so muss man zur gegenüberliegenden Seite des 3×3-Quadrats ausweichen (siehe Abbildung). Gerät man auf ein besetztes Feld, muss man direkt unter der letzten Eintragung weitermachen:
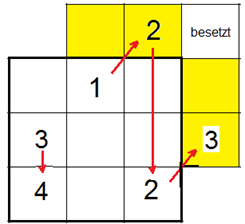
Auf diese Weise entsteht folgendes 3×3-Quadrat:
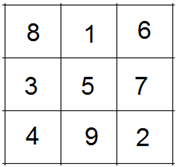
Ein 4×4-Quadrat kann man konstruieren, nachdem zunächst einige Felder markiert wurden:
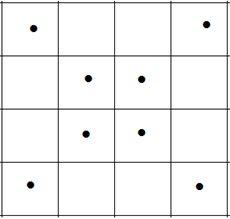
Nun werden Zeile für Zeile und von links nach rechts die Zahlen von 1 bis 16 den Feldern zugeordnet und nur dort eingetragen, wo nicht markiert wurde:
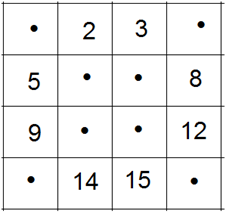
Dann werden Zeile für Zeile unten rechts beginnen und von rechts nach links die Zahlen von 1 bis 16 den Feldern zugeordnet und nur dort eingetragen, wo nicht bereits eine Zahl steht:
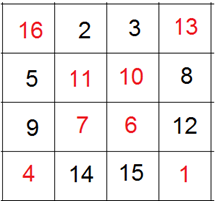
Fertig ist das 4×4-Quadrat. Daraus wird nun ein 12×12-Quadrat konstruiert, indem man jedes der 16 Quadrate mit einem 3×3-Quadrat füllt, dessen mittleres Feld der ersten Zeile mit 9k-8 beschriftet wird. k wird an der entsprechenden Stelle aus dem magischen 4×4-Quadrat übernommen:
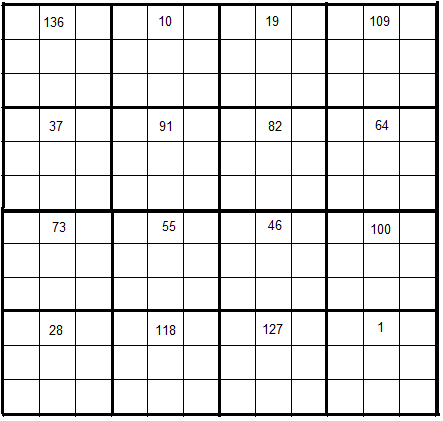
Jedes 3×3-Quadrat wird nun beginnend jeweils oben in seiner Mitte nach dem gleichen Prinzip mit den nachfolgenden Zahlen gefüllt, wie das zu Beginn genannte:
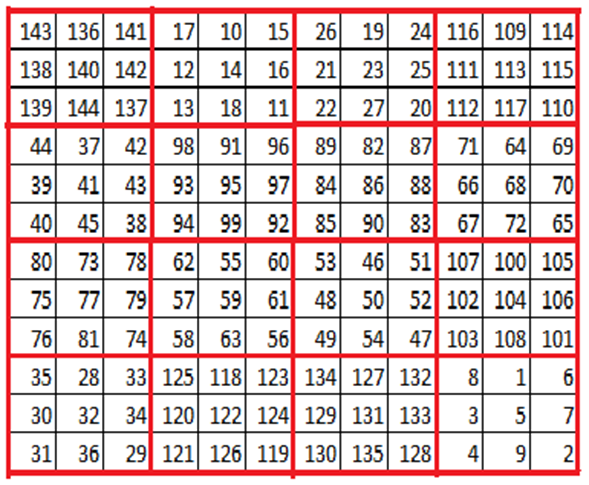
Eine andere Darstellung eines magischen 12×12-Quadrats in der andere Teilquadrate sichtbar werden, entstammt einer mathematischen Zeitschrift namens „Scripta mathematica“, welche von 1933 bis 1977 in den USA erschien. Im April 1936 veröffentlicht ein Royal v. Heath dieses Quadrat:

Darin sind vier 6×6-Quadrate (rot umrandet) mit der charakteristischen Summe 435, vier 4×4-Quadrate (grün umrandet) mit der charakteristischen Summe 290 und ein 8×8-Quadrat (gelb umrandet) mit der charakteristischen Summe 580. Leider verrät der Autor nicht, wie er sein 12×12-Quadrat konstruiert hat.